中, , ,过点 作直线 ,使 ,点 在直线 上,作射线 ,将射线 绕点 顺时针旋转角 后交直线 于点 .
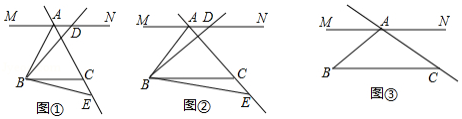
(1)如图①,当 ,且点 在射线 上时,直接写出线段 , , 的数量关系.
(2)如图②,当 ,且点 在射线 上时,直写出线段 、 、 的数量关系,并说明理由.
(3)当 时,若点 在射线 上, , ,请直接写出线段 的长度.
现有一张矩形纸片 (如图)。其中 ,点 是 的中点,将纸片沿直线 折叠,点 落在四边形 内,记为点 ,求线段 的长.

已知 ,判定以 为边的四边形的形状.
下面有四个命题:
(1)一组对边相等且一组对角相等的四边形是平行四边形.
(2)一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形.
(3)一组对角相等且这一组对角的顶点所连接的对角线平分另一条对角线的四边形是平行四边形.
(4)一组对角相等且这一组对角的顶点所连接的对角线被另一条对角线平分的四边形是平行四边形.
上述命题是否正确?正确的请证明,错误的请举出反例.
如图,在 中, 是 的中点, 于点 ,求证: .

如图①,在四边形 中, 分别是 的中点,连接 并延长,分别与 的延长线交于点 ,则 .
(温馨提示:在图①中,连接 ,取 的中点 ,连接 ,根据三角形中位线定理,证明 ,从而 ,再利用平行线性质,可证 .)
(1)如图②,在四边形 中, 与 相交于点 分别是 的中点,连接 ,分别交 于点 ,判断 的形状,并给予证明;
(2)如图③,在 中, 点在 上, 分别是 的中点,连接 并延长,与 的延长线交于 ,若 ,连接 ,判断 的形状并证明.
