已知,在 中,点 在 上,点 是 延长线上一点,且 ,连接 交 于点 .
(1)猜想证明:如图1,在 中,若 ,学生们发现: .下面是两位学生的证明思路:
思路1:过点 作 ,交 于点 ,可证 得出结论;
思路2:过点 作 ,交 的延长线于点 ,可证 得出结论;
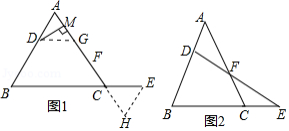
请你参考上面的思路,证明 (只用一种方法证明即可).
(2)类比探究:在(1)的条件下(如图 ,过点 作 于点 ,试探究线段 , , 之间满足的数量关系,并证明你的结论.
(3)延伸拓展:如图2,在 中,若 , , ,请你用尺规作图在图2中作出 的垂直平分线交 于点 (不写作法,只保留作图痕迹),并用含 的代数式直接表示 的值.
如图,在 中, ,点 , 分别是边 , 上的中点,连接 并延长至点 ,使 ,连接 、 .
(1)证明: ;
(2)当 时,试判断四边形 的形状并说明理由.

2017年6月2日,贵阳市生态委发布了《2016年贵阳市环境状况公报》,公报显示,2016年贵阳市生态环境质量进一步提升,小颖根据公报中的部分数据,制成了下面两幅统计图,请根据图中提供的信息,回答下列问题:
(1) , ;(结果保留整数)
(2)求空气质量等级为“优”在扇形统计图中所占的圆心角的度数;(结果精确到
(3)根据了解,今年 月贵阳市空气质量优良天数为142天,优良率为 ,与2016年全年的优良率相比,今年前五个月贵阳市空气质量的优良率是提高还是降低了?请对改善贵阳市空气质量提一条合理化建议。

下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.
解:
第一步
第二步
(1)小颖的化简过程从第 步开始出现错误;
(2)对此整式进行化简.
如图,在平面直角坐标系中,二次函数的图象交坐标轴于 , , 三点,点 是直线 下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点 ,使 是以 为底边的等腰三角形?若存在,求出 点坐标;若不存在,请说明理由;
(3)动点 运动到什么位置时, 面积最大,求出此时 点坐标和 的最大面积.

如图,已知 的直径 , , 为圆周上两点,且四边形 是平行四边形,过 点作直线 ,分别交 , 的延长线于点 , , 与 交于 点.
(1)求证: 是 的切线;
(2)求 的长.
