如图,四边形 是矩形 ,要在矩形 内作一个以 为边的正方形 ,某位同学的作法如下:
①作 的平分线 . 交 于点 ;
②以点 为圆心, 长为半径画弧,交 于点 ,连接 .
(1)求证:四边形 是正方形;
(2)若 ,求图中阴影部分的面积.

如图,在平面直角坐标系中,直线l是第一、三象限的角平分线
实验与探究: 
(1)由图观察易知A(0,2)关于直线l的对称点
 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点
的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点 、
、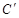 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:  、
、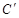 ;
;
归纳与发现:(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点
 的坐标为
的坐标为
运用与拓广:(3)已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
:某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从以下4个方案中选择合理的方案来确定每个演讲者的最后得分。
方案1:所有评委所给分的平均数.方案2:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数.
方案3:所有评委所给分的中位数.
方案4:所有评委所给分的众数.
|
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F )、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题: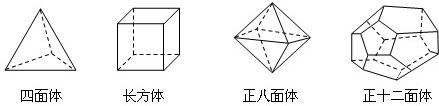
(1)根据上面多面体模型,完成表格中的空格:
| 多面体 |
顶点数(V) |
面数(F) |
棱数(E) |
| 四面体 |
4 |
4 |
6 |
| 长方体 |
8 |
6 |
12 |
| 正八面体 |
6 |
8 |
12 |
| 正十二面体 |
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是
(3)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是
(4)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,x+y=
(本题6分)点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.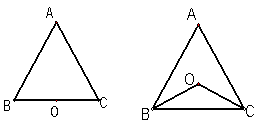
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
某住宅小区在住宅建设时留下一块1798平方米的空地,准备建一个矩形的露天游泳池,设计如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带请你计算出游泳池的长和宽
若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,请你计算要贴瓷砖的总面积
