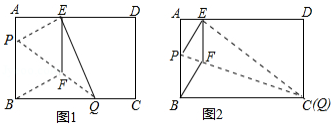
如图1,在矩形纸片 中, , ,折叠纸片使 点落在边 上的 处,折痕为 ,过点 作 交 于 ,连接 .
(1)求证:四边形 为菱形;
(2)当点 在 边上移动时,折痕的端点 、 也随之移动;
①当点 与点 重合时(如图 ,求菱形 的边长;
②若限定 、 分别在边 、 上移动,求出点 在边 上移动的最大距离.
某大型快递公司使用机器人进行包裹分拣,若甲机器人工作 ,乙机器人工作 ,一共可以分拣700件包裹;若甲机器人工作 ,乙机器人工作 ,一共可以分拣650件包裹.
(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)“双十一”期间,快递公司的业务量猛增,要让甲、乙两机器人每天分拣包裹的总数量不低于2250件,它们每天至少要一起工作多少小时?
某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
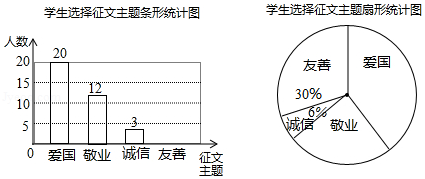
(1)求本次调查共抽取了多少名学生的征文;
(2)将上面的条形统计图和扇形统计图补充完整;
(3)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名;
(4)本次抽取的3份以“诚信”为主题的征文分别是小义、小玉和大力的,若从中随机选取2份以“诚信”为主题的征文进行交流,请用画树状图法或列表法求小义和小玉同学的征文同时被选中的概率.
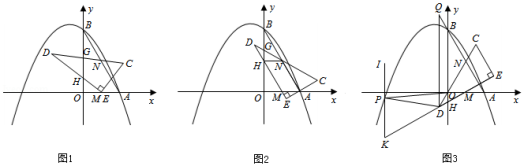
如图1,在平面直角坐标系中, 是坐标原点,抛物线 与 轴正半轴交于点 ,与 轴交于点 ,连接 ,点 , 分别是 , 的中点, ,且 始终保持边 经过点 ,边 经过点 ,边 与 轴交于点 ,边 与 轴交于点 .
(1)填空: 的长是 , 的度数是 度;
(2)如图2,当 ,连接 .
①求证:四边形 是平行四边形;
②判断点 是否在该抛物线的对称轴上,并说明理由;
(3)如图3,当边 经过点 时,(此时点 与点 重合),过点 作 ,交 延长线上于点 ,延长 到点 ,使 ,过点 作 ,在 上取一点 ,使得 (点 , 在直线 的同侧),连接 ,请直接写出 的长.
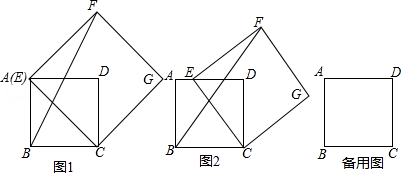
四边形 是边长为4的正方形,点 在边 所在直线上,连接 ,以 为边,作正方形 (点 ,点 在直线 的同侧),连接 .
(1)如图1,当点 与点 重合时,请直接写出 的长;
(2)如图2,当点 在线段 上时, ;
①求点 到 的距离;
②求 的长;
(3)若 ,请直接写出此时 的长.
如图,在平面直角坐标系中,四边形 的顶点 是坐标原点,点 的坐标为 ,点 的坐标为 ,点 的坐标为 , ,点 , 分别为四边形 边上的动点,动点 从点 开始,以每秒1个单位长度的速度沿 路线向终点 匀速运动,动点 从 点开始,以每秒两个单位长度的速度沿 路线向终点 匀速运动,点 , 同时从 点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间 秒 , 的面积为 .
(1)填空: 的长是 , 的长是 ;
(2)当 时,求 的值;
(3)当 时,设点 的纵坐标为 ,求 与 的函数关系式;
(4)若 ,请直接写出此时 的值.
