如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,点 坐标为 ,点 坐标为 ,点 是抛物线的顶点,过点 作 轴的垂线,垂足为 ,连接 .
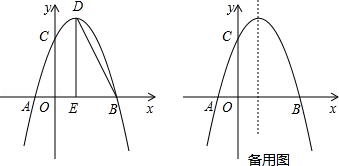
(1)求抛物线的解析式及点 的坐标;
(2)点 是抛物线上的动点,当 时,求点 的坐标;
(3)若点 是抛物线上的动点,过点 作 轴与抛物线交于点 ,点 在 轴上,点 在坐标平面内,以线段 为对角线作正方形 ,请写出点 的坐标.
如图,已知EF∥AD,∠1=∠2,∠BAC=65º.请将求∠AGD的过程填写完整.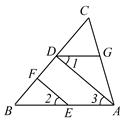
解:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
(本题10分)
如图,在△ABC中,∠C=90º,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.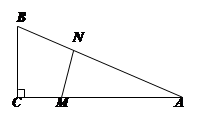
(1)当t为何值时,△AMN的面积为6米2?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
阅读材料:如果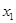 、
、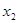 是一元二次方程
是一元二次方程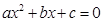 (
(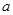 ≠0)的两根,那么,
≠0)的两根,那么,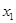 +
+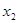 =
=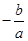 ,
,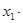
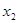 =
=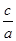 .这就是著名的韦达定理.
.这就是著名的韦达定理.
现在我们利用韦达定理解决问题:
已知 与
与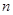 是方程
是方程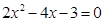 的两根,
的两根,
(1)填空: +
+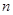 =________;
=________;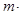
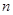 =________;
=________;
(2)计算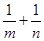 的值.
的值.
(本题8分)
在如图的4×4的方格内画△ABC,使它的顶点都在格点上,三条边长分别为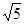 ,
,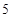 ,
, .
.
(本题8分)
已知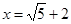 ,
,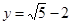 ,求下列各式的值:
,求下列各式的值:
(1)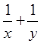 ;
;
(2)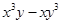 .
.