某班级同学从学校出发去扎龙自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人 后乘坐小轿车沿同一路线出行.大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的 继续行驶,小轿车保持原速度不变.小轿车司机因路线不熟错过了景点入口,在驶过景点入口 时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程 (单位: 和行驶时间 (单位: 之间的函数关系如图所示.
请结合图象解决下面问题:
(1)学校到景点的路程为 ,大客车途中停留了 , ;
(2)在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
(3)小轿车司机到达景点入口时发现本路段限速 ,请你帮助小轿车司机计算折返时是否超速?
(4)若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待 分钟,大客车才能到达景点入口.

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需元,购买12根跳绳需元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
如图,点A、O、E在同一条直线上,且∠AOB=40°, ∠EOD=30°,OD平分∠COE,求∠COB的度数。
先化简,再求值:5(3a2b-ab2)-4(-ab2+3a2b), 其中a=-1,b=-2.
解方程:(每小题5分,共10分)
① 3x-7(x-1)=3-2(x+3)
②
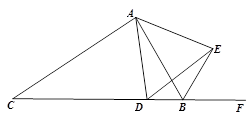
已知:如图,△ABC中,点D是BC边上的一点,∠ADE=∠ABC=60°,DE交∠ABC的外角平分线于点E.求证:△ADE是等边三角形.