随着地铁和共享单车的发展,“地铁 单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的 , , , , 中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为 (单位:千米),乘坐地铁的时间 (单位:分钟)是关于 的一次函数,其关系如下表:
地铁站 |
|
|
|
|
|
(千米) |
8 |
9 |
10 |
11.5 |
13 |
(分钟) |
18 |
20 |
22 |
25 |
28 |
(1)求 关于 的函数表达式;
(2)李华骑单车的时间(单位:分钟)也受 的影响,其关系可以用 来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
如图, , 为 中点,点 在线段 上(不与点 , 重合),将 绕点 逆时针旋转 后得到扇形 , , 分别切优弧 于点 , ,且点 , 在 异侧,连接 .
(1)求证: ;
(2)当 时,求 的长(结果保留 ;
(3)若 的外心在扇形 的内部,求 的取值范围.

发现 任意五个连续整数的平方和是5的倍数.
验证 (1) 的结果是5的几倍?
(2)设五个连续整数的中间一个为 ,写出它们的平方和,并说明是5的倍数.
延伸 任意三个连续整数的平方和被3除的余数是几呢?请写出理由.
编号为 号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为 .
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
(2)在这6名学生中,随机选一名学生,求选上命中率高于 的学生的概率;
(3)最后,又来了第7号学生,也按同样记分规定投了5次,这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.

在一条不完整的数轴上从左到右有点 , , ,其中 , ,如图所示,设点 , , 所对应数的和是 .
(1)若以 为原点,写出点 , 所对应的数,并计算 的值;若以 为原点, 又是多少?
(2)若原点 在图中数轴上点 的右边,且 ,求 .

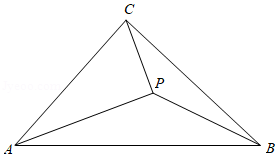
如图, 中, , , 为 内部一点,且 .
(1)求证: ;
(2)求证: ;
(3)若点 到三角形的边 , , 的距离分别为 , , ,求证 .