如图1,点 坐标为 ,以 为边在第一象限内作等边 ,点 为 轴上一动点,且在点 右侧,连接 ,以 为边在第一象限内作等边 ,连接 交 于 .
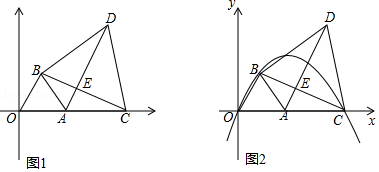
(1)①直接回答: 与 全等吗?
②试说明:无论点 如何移动, 始终与 平行;
(2)当点 运动到使 时,如图2,经过 、 、 三点的抛物线为 .试问: 上是否存在动点 ,使 为直角三角形且 为直角边?若存在,求出点 坐标;若不存在,说明理由;
(3)在(2)的条件下,将 沿 轴翻折得 ,设 与 组成的图形为 ,函数 的图象 与 有公共点.试写出: 与 的公共点为3个时, 的取值.
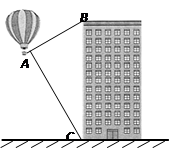
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为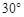 ,看这栋高楼底部的俯角为
,看这栋高楼底部的俯角为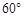 ,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据:
,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据: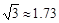 )
)
在 ABCD中,E,F分别是BC、AD上的点,且BE=DF.求证:AE=CF.
ABCD中,E,F分别是BC、AD上的点,且BE=DF.求证:AE=CF.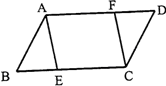
先化简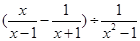 ,再从
,再从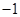 、
、 、
、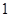 三个数中,选择一个你认为合适的数作为
三个数中,选择一个你认为合适的数作为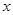 的值代入求值.
的值代入求值.
计算: .
.
已知二次函数y=-x2+2x+图象交x轴于点A,B(A在B的左侧),交y轴于点C,点D是该函数图像上一点,且点D的横坐标为3,连接BD.点E是线段AB上一动点(不与点A重合),过E作EF⊥AB交射线AD于点F,以EF为一边在EF的右侧作正方形EFGH.设E点的坐标为(t,0).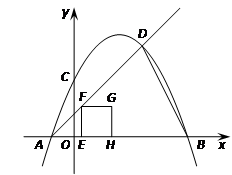
](1)求射线AD的解析式;
(2)在线段AB上是否存在点E,使△OCG为等腰三角形?
若存在,求正方形EFGH的边长;若不存在,请说明理由;
(3)设正方形EFGH与△ABD重叠部分面积为S,求S与t的函数关系式.