(阅读)
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
(理解)
(1)如图1,两个直角边长分别为 、 、斜边长为 的直角三角形和一个两条直角边都是 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ;
(运用)
(3) 边形有 个顶点,在它的内部再画 个点,以 个点为顶点,把 边形剪成若干个三角形,设最多可以剪得 个这样的三角形.当 , 时,如图3,最多可以剪得7个这样的三角形,所以 .
①当 , 时,如图4, ;当 , 时, ;
②对于一般的情形,在 边形内画 个点,通过归纳猜想,可得 (用含 、 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.

(1)计算:
(2)先化简,再求值: ,其中
,其中 。
。
如图,已知△ABC中,AB="AC=6" cm, ,BC="4" cm,点D为AB的中点
,BC="4" cm,点D为AB的中点如果点P在线段BC上以1 cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,
请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使
△BPD与△CQP全等?若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

某汉堡店员工小李去两户家庭外送汉堡包和澄汁,第一家送3个汉堡包和2杯橙汁,向顾客收取了32元,第二家送2个汉堡包和3杯橙汁,向顾客收取了28元如果汉堡店员工外送4个汉堡包和5杯橙汁,那么他应收顾客多少元钱?
若有顾客同时购买汉堡包和橙汁且购买费用恰好为20元,问汉堡店该如何配送?
如图,线段AC、BD相交于点O,OA=OC,OB=OD.
△OAB 与△OCD全等吗?为什么?
过点O任意作一条与AB、AC都相交的直线MN,交点分别为M、N,OM与ON相等吗?为什么?
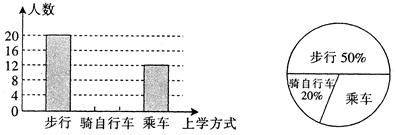
学习了统计知识后,小明的数学老师要求每个学生就本班同学的上学方式进行一次调查统计,如图是小明通过收集数据后绘制的两幅不完整的统计图.请根据图中提供的信息,解答下列问题:该班共有_______________名学生;
将“骑自行车”部分的条形统计图补充完整;
在扇形统计图中;求出“乘车”部分所对应的圆心角的度数;
若全年级有600名学生,试估计该年级骑自行车上学的学生人数.