某汉堡店员工小李去两户家庭外送汉堡包和澄汁,第一家送3个汉堡包和2杯橙汁,向顾客收取了32元,第二家送2个汉堡包和3杯橙汁,向顾客收取了28元如果汉堡店员工外送4个汉堡包和5杯橙汁,那么他应收顾客多少元钱?
若有顾客同时购买汉堡包和橙汁且购买费用恰好为20元,问汉堡店该如何配送?
一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆成如下右图形式,使点B、F、C、D在同一条直线上。求证AB⊥ED;
若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明。(考查逻辑推理能力)

如下图,路灯下,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN。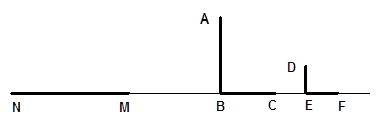
试确定路灯的位置(用点P表示)
在图中画出表示大树高的线段。(考查投影等)
若小明的眼睛看成是点D,试画图分析小明能否看见大树
解方程: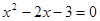 (考查一元二次方程的解法)
(考查一元二次方程的解法)
如图,在平行四边形ABCD中,AB在x轴上,D点y轴上,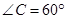 ,
, ,B点坐标为(4,0).点
,B点坐标为(4,0).点 是边
是边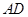 上一点,且
上一点,且 .点
.点 、
、 分别从
分别从 、
、 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿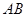 、
、 向点
向点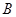 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为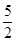 ,设运动时间为
,设运动时间为 秒。
秒。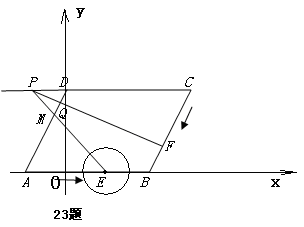
求直线BC的解析式。
当
 为何值时,
为何值时, ?
?在(2)问条件下,⊙E与直线PF是否相切;如果相切,加以证明,并求出切点的坐标。如果不相切,说明理由。
在梯形ABCD中,AB∥CD,∠BCD=90,且AB=1,BC=2,tan∠ADC=2;对角线相交于O点,等腰直角三角板的直角顶点落在梯形的顶点C上,使三角板绕点C旋转。
当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=
 时,求PE及DH的长。
时,求PE及DH的长。