为了解同学们最喜欢一年四季中的哪个季节,数学社在全校随机抽取部分同学进行问卷调查,根据调查结果,得到如下两幅不完整的统计图.

根据图中信息,解答下列问题:
(1)此次调查一共随机抽取了 名同学;扇形统计图中,“春季”所对应的扇形的圆心角的度数为 ;
(2)若该学校有1500名同学,请估计该校最喜欢冬季的同学的人数;
(3)现从最喜欢夏季的3名同学 , , 中,随机选两名同学去参加学校组织的“我爱夏天”演讲比赛,请用列表或画树状图的方法求恰好选到 , 去参加比赛的概率.
(1)计算: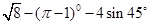 ;
;
(2)解不等式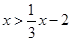 ,并将其解集表示在数轴上.
,并将其解集表示在数轴上.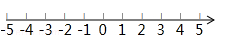
一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
(攀枝花)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
(巴中)解不等式: ,并把解集表示在数轴上.
,并把解集表示在数轴上.
(广元)经统计分析.某市跨河大桥上的车流速度v(千米/时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞.此时车流速度为0千米/时;当车流密度不超过20辆/千米,车流速度为80千米/时.研究表明:当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在某一交通时段.为使大桥上的车流速度大于60千米/时且小于80千米/时,应把大桥上的车流密度控制在什么范围内?