某汽车运输公司为了满足市场需要，推出商务车和轿车对外租赁业务-优题课

题文

某汽车运输公司为了满足市场需要，推出商务车和轿车对外租赁业务．下面是乐山到成都两种车型的限载人数和单程租赁价格表：

（1）如果单程租赁2辆商务车和3辆轿车共需付租金1320元，求一辆轿车的单程租金为多少元？

（2）某公司准备组织34名职工从乐山赴成都参加业务培训，拟单程租用商务车或轿车前往．在不超载的情况下，怎样设计租车方案才能使所付租金最少？

科目数学题型解答题难度中等

知识点：二元一次方程组的应用一次函数的应用

相关试题

如图，在菱形 $ABCD$ 中， $∠ A = 110 °$ ，点 $E$ 是菱形 $ABCD$ 内一点，连结 $CE$ 绕点 $C$ 顺时针旋转 $110 °$ ，得到线段 $CF$ ，连结 $BE$ ， $DF$ ，若 $∠ E = 86 °$ ，求 $∠ F$ 的度数．

某校为了丰富学生的课外体育活动，购买了排球和跳绳．已知排球的单价是跳绳的单价的3倍，购买跳绳共花费750元，购买排球共花费900元，购买跳绳的数量比购买排球的数量多30个，求跳绳的单价．

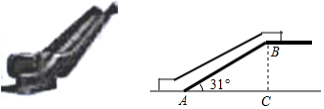
如图，某商店营业大厅自动扶梯 $AB$ 的倾斜角为 $31 °$ ， $AB$ 的长为12米，求大厅两层之间的距离 $BC$ 的长．（结果精确到0.1米）（参考数据： $\sin 31 ° = 0.515$ ， $\cos 31 ° = 0.857$ ， $\tan 31 ° = 0.60)$

一个不透明的口袋中有三个小球，上面分别标有字母 $a$ ， $b$ ， $c$ ，每个小球除字母不同外其余均相同，小园同学从口袋中随机摸出一个小球，记下字母后放回且搅匀，再从可口袋中随机摸出一个小球记下字母．用画树状图（或列表）的方法，求小园同学两次摸出的小球上的字母相同的概率．

如图1，在平面直角坐标系中，点 $B$ 在 $x$ 轴正半轴上， $OB$ 的长度为 $2 m$ ，以 $OB$ 为边向上作等边三角形 $AOB$ ，抛物线 $l : y = a x^{2} + bx + c$ 经过点 $O$ ， $A$ ， $B$ 三点

（1）当 $m = 2$ 时， $a =$ 　　，当 $m = 3$ 时， $a =$ 　　；

（2）根据（1）中的结果，猜想 $a$ 与 $m$ 的关系，并证明你的结论；

（3）如图2，在图1的基础上，作 $x$ 轴的平行线交抛物线 $l$ 于 $P$ 、 $Q$ 两点， $PQ$ 的长度为 $2 n$ ，当 $ΔAPQ$ 为等腰直角三角形时， $a$ 和 $n$ 的关系式为　　；

（4）利用（2）（3）中的结论，求 $ΔAOB$ 与 $ΔAPQ$ 的面积比．