如图,点 、 分别是等边 边 、 上的动点(端点除外),点 、点 以相同的速度,同时从点 、点 出发.
(1)如图1,连接 、 .求证: ;
(2)如图1,当点 、 分别在 、 边上运动时, 、 相交于点 , 的大小是否变化?若变化,请说明理由;若不变,求出它的度数;
(3)如图2,当点 、 在 、 的延长线上运动时,直线 、 相交于 , 的大小是否变化?若变化,请说明理由;若不变,求出它的度数.

某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.

请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为 人,其中“非常满意”的人数为 人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众均来自甲片区的概率.
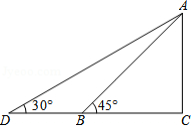
某小区为了安全起见,决定将小区内的滑滑板的倾斜角由 调为 ,如图,已知原滑滑板 的长为4米,点 , , 在同一水平地面上,调整后滑滑板会加长多少米?(结果精确到0.01米,参考数据: , ,
如图,在等腰直角三角形 中, ,点 在 轴上,点 在 轴上,点 ,二次函数 的图象经过点 .
(1)求二次函数的解析式,并把解析式化成 的形式;
(2)把 沿 轴正方向平移,当点 落在抛物线上时,求 扫过区域的面积;
(3)在抛物线上是否存在异于点 的点 ,使 是以 为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点 的坐标;如果不存在,请说明理由.

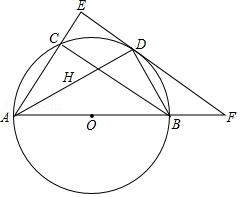
如图,在直角三角形 中, ,点 是 的内心,
的延长线和三角形 的外接圆 相交于点 ,连接 .
(1)求证: ;
(2)过点 作 的平行线交 、 的延长线分别于点 、 ,已知 ,圆 的直径为5.
①求证: 为圆 的切线;
②求 的长.
为配合“一带一路”国家倡议,某铁路货运集装箱物流园区正式启动了2期扩建工程.一项地基基础加固处理工程由 、 两个工程公司承担建设,已知 工程公司单独建设完成此项工程需要180天, 工程公司单独施工45天后, 工程公司参与合作,两工程公司又共同施工54天后完成了此项工程.
(1)求 工程公司单独建设完成此项工程需要多少天?
(2)由于受工程建设工期的限制,物流园区管委会决定将此项工程划包成两部分,要求两工程公司同时开工, 工程公司建设其中一部分用了 天完成, 工程公司建设另一部分用了 天完成,其中 , 均为正整数,且 , ,求 、 两个工程公司各施工建设了多少天?