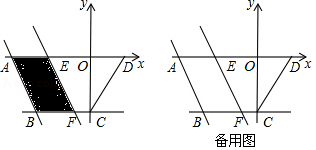
如图,在平面直角坐标系中,四边形 的边 在 轴上,点 在 轴的负半轴上,直线 ,且 , ,将经过 、 两点的直线 向右平移,平移后的直线与 轴交于点 ,与直线 交于点 ,设 的长为 .
(1)四边形 的面积为 ;
(2)设四边形 被直线 扫过的面积(阴影部分)为 ,请直接写出 关于 的函数解析式;
(3)当 时,直线 上有一动点 ,作 直线 于点 ,交 轴于点 ,将 沿直线 折叠得到 ,探究:是否存在点 ,使点 恰好落在坐标轴上?若存在,请求出点 的坐标;若不存在,请说明理由.
先化简,再求值: ,其中 为整数且满足不等式组 .
先化简,再求值: ,其中 、 满足 .
计算: .
已知抛物线 经过点 , 、 与 轴交于另一点 ,连接 .
(1)求抛物线的解析式;
(2)如图, 是第一象限内抛物线上一点,且 ,求证: ;
(3)在抛物线上是否存在点 ,直线 交 轴于点 ,使 与以 , , , 中的三点为顶点的三角形相似(不重合)?若存在,请求出点 的坐标;若不存在,请说明理由.

已知正方形 与正方形 , 是 的中点,连接 , .
(1)如图1,点 在 上,点 在 的延长线上,请判断 , 的数量关系与位置关系,并直接写出结论;
(2)如图2,点 在 的延长线上,点 在 上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形 绕点 旋转,使 , , 三点在一条直线上,若 , ,请画出图形,并直接写出 的长.
