攀枝花芒果由于品质高、口感好而闻名全国,通过优质快捷的网络销售渠道,小明的妈妈先购买了2箱 品种芒果和3箱 品种芒果,共花费450元;后又购买了1箱 品种芒果和2箱 品种芒果,共花费275元(每次两种芒果的售价都不变).
(1)问 品种芒果和 品种芒果的售价分别是每箱多少元?
(2)现要购买两种芒果共18箱,要求 品种芒果的数量不少于 品种芒果数量的2倍,但不超过 品种芒果数量的4倍,请你设计购买方案,并写出所需费用最低的购买方案.
在锐角△ABC中,AB=AC,∠A使关于x的方程
 -sinA x+
-sinA x+ sinA-
sinA- =0有两个相等的实数根.
=0有两个相等的实数根.判断△ABC的形状;
设D为BC上的一点,且DE⊥AB于E,DF⊥AC于F,若DE=m,DF=n,且3m=4n和m2+n2=25,求AB的长.
某旅游公司拟在暑假期间面向学生推出“杭州一日游”活动,收费标准如下:
| 人数m |
0<m≤100 |
100<m≤200 |
m>200 |
| 收费标准(元/人) |
90 |
85 |
75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动。已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元。两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
两所学校报名参加旅游的学生各有多少人?
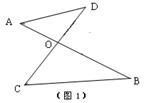
已知如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”. 那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥聪明才智,解决以下问题:在图1中,请写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;
仔细观察,在图2中“8”字形”的个数个;
在图2中,若∠D=400,∠B=360,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;

如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)。
如图(1),点A、B、C在同一直线上,且△ABE, △BCD都是等边三角形,连结AD,CE.△BEC可由△ABD顺时针旋转得到吗?若是,请描述这一旋转变换过程;若不是,请说明理由;
若△BCD绕点B顺时针旋转,使点A,B,C不在同一直线上(如图(2)),则在旋转过程中:
①线段AD与EC的长度相等吗?请说明理由.
②锐角 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出 的度数;若改变,请说明理由.
的度数;若改变,请说明理由.
(注:等边三角形的三条边都相等,三个内角都是60°)

如图,有牌面数字都是2,3,4的两组牌.从每组牌中各随机摸出一张,请用画树状图或列表的方法,求摸出的两张牌的牌面数字之和为6的概率. 