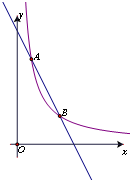
某网络约车公司近期推出了”520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图(如图).
组别 |
单次营运里程“ ”(公里) |
频数 |
第一组 |
|
72 |
第二组 |
|
|
第三组 |
|
26 |
第四组 |
|
24 |
第五组 |
|
30 |
根据统计表、图提供的信息,解答下面的问题:
(1)①表中 ;②样本中“单次营运里程”不超过15公里的频率为 ;③请把频数分布直方图补充完整;
(2)请估计该公司这5000个“单次营运里程”超过20公里的次数;
(3)为缓解城市交通压力,维护交通秩序,来自某市区的4名网约车司机 男1女)成立了“交通秩序维护”志愿小分队,若从该小分队中任意抽取两名司机在某一路口维护交通秩序,请用列举法(画树状图或列表)求出恰好抽到“一男一女”的概率.

(本小题满分7分,其中(1)小题3分,(2)小题4分)
解下列二元一次方程组:
(1)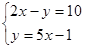
(2)
已知二次函数y=ax2+bx+c的图象的顶点坐标为 (0,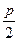 ),且 ac=
),且 ac=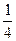 .
.
(1)若该函数的图象经过点(-1,-1).
①求使y<0成立的x的取值范围.
②若圆心在该函数的图象上的圆与x轴、y轴都相切,求圆心的坐标.
(2)经过A(0,p)的直线与该函数的图象相交于M,N两点,过M,N作x轴的垂线,垂足分别为M1,N1,设△MAM1,△A M1N1,△ANN1的面积分别为s1,s2,s3,是否存在m,使得对任意实数p≠0都有s22=ms1s3成立,若存在,求出m的值,若不存在,请说明理由.
M1N1,△ANN1的面积分别为s1,s2,s3,是否存在m,使得对任意实数p≠0都有s22=ms1s3成立,若存在,求出m的值,若不存在,请说明理由.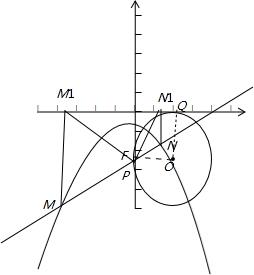
如图,点P为等边△ABC外接圆劣弧BC上一点.
(1)求∠BPC的度数;
(2)求证:PA=PB+PC;
(3)设PA,BC交于点M,若AB=4,PC=2,求CM的长度.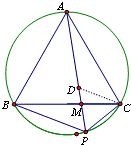
如图,一艘船以每小时60海里的速度自A向正北方向航行,船在A处时,灯塔S在船的北偏东30°,航行1小时后到B处,此时灯塔S在船的北偏东75°,(运算结果保留根号)
(1)求船在B处时与灯塔S的距离;
(2)若船从B处继续向正北方向航行,问经过多长时间船与灯塔S的距离最近.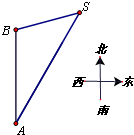
如图,已知函数y= 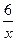 (x>0)的图象与一次函数y=kx+b的图象交于点A(1,m),B(n,2)两点.
(x>0)的图象与一次函数y=kx+b的图象交于点A(1,m),B(n,2)两点.
(1)求一次函数的解析式;
(2)将一次函数y=kx+b的图象沿x轴负方向平移a(a>0)个单位长度得到新图象,求这个新图象与函数 y=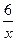 (x>0)的图象只有一个交点M时a的值及交点M的坐标.
(x>0)的图象只有一个交点M时a的值及交点M的坐标.