如图,已知抛物线 与直线 交于 , 两点,交 轴于 、 两点,连接 、 ,已知 , .
(1)求此抛物线的解析式;
(2)在抛物线对称轴 上找一点 ,使 的值最大,并求出这个最大值;
(3)点 为 轴右侧抛物线上一动点,连接 ,过点 作 交 轴于点 ,问:是否存在点 ,使得以 , , 为顶点的三角形与 相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.

如图,矩形ABCD中,点E是BC上一点,AD=DE,AF⊥DE,垂足为F. 求证:AF=AB.
解方程:
如图,在平面直角坐标系中,已知抛物线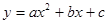 交
交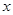 轴于
轴于 两点,交
两点,交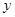 轴于点
轴于点 .
.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交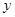 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧  的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于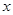 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).
(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上。B、C点在地面OM线上(如图2所示).为了筹备材料,需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.
如图,在Rt△ABC中,∠ACB=90°,AC=9cm,BC=12cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
(1)求点P到直线AB的距离;
(2)当t=1.8时,判断直线AB与⊙P的位置关系,并说明理由;
(3)已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.