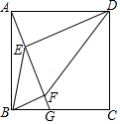
如图,在正方形 中,点 在边 上(不与点 , 重合),连接 ,作 于点 , 于点 ,设 .
(1)求证: .
(2)连接 , ,设 , .求证: .
(3)设线段 与对角线 交于点 , 和四边形 的面积分别为 和 ,求 的最大值.
某景点的门票价格规定如下表
| 购票人数 |
1—50人 |
51—100人 |
100人以上 |
| 每人门票价 |
12元 |
10元 |
8元 |
某校八年(1)(2)两班共102人去游览该景点,其中(1)班不足50人,(2)班多于50人,如果两班都以班为单位分别购票,则一共付款1118元
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
如图所示,已知矩形ABCD中,AD=8cm,AB=6cm,对角线AC的垂直平分线交AD于E,交BC于F.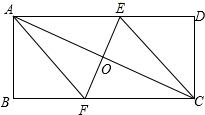
(1)试判断四边形AFCE是怎样的四边形;
(2)求出四边形AFCE的周长.
阅读下列材料:如图(1)在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为“筝形”
解答问题:如图(2)将正方形ABCD绕着点B逆时针旋转一定角度后,得到正方形GBEF,边AD与EF相交于点H.请你判断四边形ABEH是否是“筝形”,说明你的理由.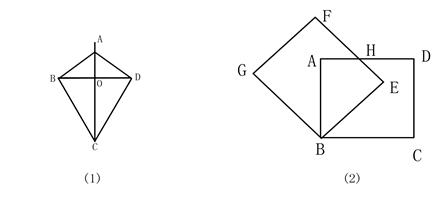
已知点A(2,2),B(-4,2),C(-2,-1),D(4,-1).在如图所示的平面直角坐标系中描出点A、B、C、D,然后依次连结A、B、C、D得到四边形ABCD,试判断四边形ABCD的形状,并说明理由.
某校教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了下表
| 零花钱数额/元 |
5 |
10 |
15 |
20 |
| 学生人数 |
10 |
15 |
20 |
5 |
(1)求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数;
(2)你认为(1)中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适?简要说明理由.