小敏思考解决如下问题:
原题:如图1,点 , 分别在菱形 的边 , 上, ,求证: .
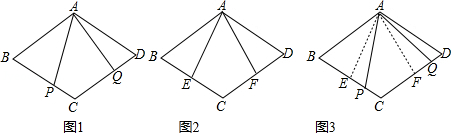
(1)小敏进行探索,若将点 , 的位置特殊化;把 绕点 旋转得到 ,使 ,点 , 分别在边 , 上,如图2.此时她证明了 ,请你证明.
(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为 , .请你继续完成原题的证明.
(3)如果在原题中添加条件: , ,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
(1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(2)列方程(组)或不等式(组)解应用题:2015年的5月20日是第15个中国学生营养日,我市某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如表).
若这份快餐中所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%,求这份快餐最多含有多少克的蛋白质?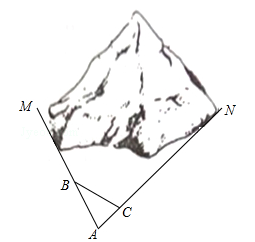
如图,两个全等的△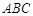 和△
和△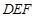 重叠在一起,固定△
重叠在一起,固定△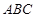 ,将△
,将△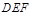 进行如下变换:
进行如下变换:
(1)如图1,△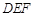 沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出
沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出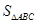 与
与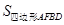 的关系;
的关系;
(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△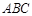 应满足什么条件?请给出证明;
应满足什么条件?请给出证明;
(3)在(2)的条件下,将△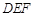 沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你在图3的位置画出图形,并求出
沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你在图3的位置画出图形,并求出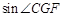 的值.
的值.
(本小题满分11分)
如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.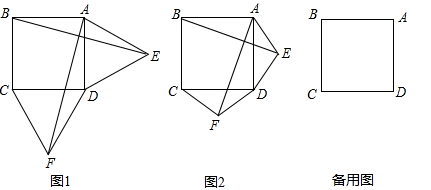
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
(本小题满分10分)如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F.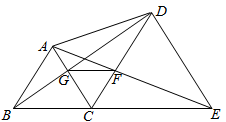
求证:(1)△ACE≌△BCD;
(2)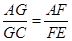 .
.
((本小题满分6分)
小颖和小丽做“摸球”游戏:在一个不透明的袋子中装有编号为1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字。若两次数字之和大于5,则小颖胜,否则小丽胜。这个游戏对双方公平吗?请说明理由。