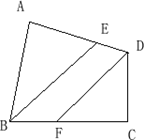
【发现】如图①,已知等边 ,将直角三角板的 角顶点 任意放在 边上(点 不与点 、 重合),使两边分别交线段 、 于点 、 .
(1)若 , , ,则 ;
(2)求证: .
【思考】若将图①中的三角板的顶点 在 边上移动,保持三角板与边 、 的两个交点 、 都存在,连接 ,如图②所示,问:点 是否存在某一位置,使 平分 且 平分 ?若存在,求出 的值;若不存在,请说明理由.
【探索】如图③,在等腰 中, ,点 为 边的中点,将三角形透明纸板的一个顶点放在点 处(其中 ,使两条边分别交边 、 于点 、 (点 、 均不与 的顶点重合),连接 .设 ,则 与 的周长之比为 (用含 的表达式表示).

如图,某班教室有9排5列座位,请根据下面4位同学的描述,在图中标出“5号“小明的位置。1号同学说:“小明在我的后方”,2号同学说:“小明在我的左后方”,3号同学说:“小明在我的左前方”,4号同学说:“小明离1号同学和3号同学的距离一样远”。说明理由。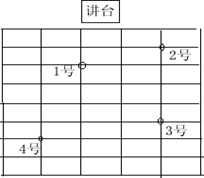
如图,点A、C分别是线段BE、BD上的一点,连接AC、EC、AD,试说明∠CAD+∠ACE+∠B+∠D+∠E=180°。
如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=64°,求∠BAC的度数
在平面直角坐标系中,已知A(—3,0),B(2,6),在X轴上求一点C使△ABC的面积为6。
如图,∠A=∠C=90°,BE,DF分别为∠ABC与∠ADC的平分线,你能判断BE∥DF吗?试说明理由