某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米.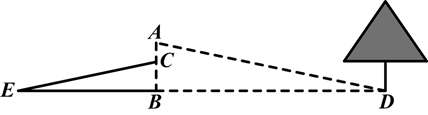
如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ,建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,小亮从胜利街的A处,沿着AB的方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在的位置(用点C标出);
(2)已知MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.
如图所示,学校操场上有一旗杆AB,甲在操场上的C处直立一根3米高的竹竿CD,甲从C处退后3米到达E处,恰好看到竹竿的顶端D与旗杆的顶端B重合,甲的眼睛到地面的距离FE为1.5米,身高相同的乙在C1处也直立一根3米高的竹竿C1D1,乙从C1处退后4米到达E1处,恰好看到竹竿的顶端D1与旗杆的顶端B也重合(点A,C,E,C1,E1在同一条直线上),量得EE1=6米,求旗杆AB的高.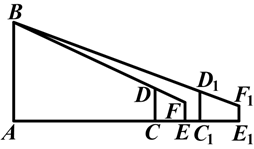
如图,甲楼高16米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时,1米长的标杆的影长是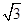 米,此时.
米,此时.
(1)如果两楼相距20米,那么甲楼的影子落在乙楼上有多高?
(2)如果甲楼的影子刚好不落在乙楼上,那么两楼的距离是多少?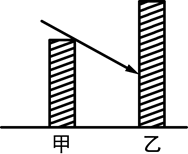
如图所示,直立在点B处的标杆AB长2.5米,观察者站在点F处,人眼E、标杆顶A、树顶C在同一条直线上,点F,B,D也在同一条直线上.已知BD=10米,FB=3米,EF=1.7米,求树高DC.(结果保留一位小数)