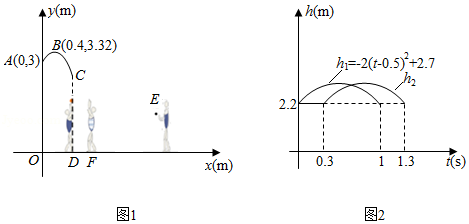
在篮球比赛中,东东投出的球在点 处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点 .
(1)求该抛物线的函数表达式.
(2)当球运动到点 时被东东抢到, 轴于点 , .
①求 的长.
②东东抢到球后,因遭对方防守无法投篮,他在点 处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点 .东东起跳后所持球离地面高度 (传球前)与东东起跳后时间 满足函数关系式 ;小戴在点 处拦截,他比东东晚 垂直起跳,其拦截高度 与东东起跳后时间 的函数关系如图2所示(其中两条抛物线的形状相同).东东的直线传球能否越过小戴的拦截传到点 ?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计).
(本题6分) 已知:如图,在△ABC中, D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.

(1)求证:D是BC的中点;

(2)如果AB=AC,试判断四边形ADCF的
 形状,并证明你的结论.
形状,并证明你的结论.
(本题6分)
求不等式组 的整数解.
的整数解.
P点为抛物线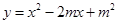 (
(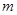 为常数,
为常数,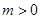 )上任一点,将抛物线绕顶点
)上任一点,将抛物线绕顶点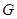 逆时针旋转
逆时针旋转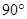 后得到的新图象与
后得到的新图象与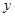 轴交于
轴交于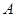 、
、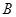 两点(点
两点(点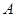 在点
在点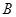 的上方),点
的上方),点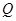 为点
为点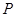 旋转后的对应点.
旋转后的对应点.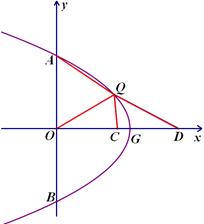
(1)当
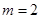 ,点
,点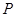 横坐标为4时,求
横坐标为4时,求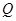 点的坐标;
点的坐标;(2)设点
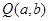 ,用含
,用含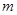 、
、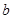 的代数式表示
的代数式表示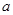 ;
;(3) 如图,点
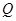 在第一象限内, 点
在第一象限内, 点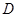 在
在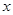 轴的正半轴上,点
轴的正半轴上,点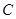 为
为 的中点,
的中点,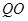 平分
平分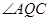 ,
,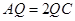 ,当
,当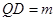 时,求
时,求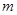 的值.
的值.
有六个学生分成甲、乙两组(每组三个人),分乘两辆出租车同时从学校出发去距学校60km的博物馆参观,10分钟后到达距离学校12km处有一辆汽车出现故障,接着正常行驶的一辆车先把第一批学生送到博物馆再回头接第二批学生,同时第二批学生步行12km后停下休息10分钟恰好与回头接他们的小汽车相遇,当第二批学生到达博物馆时,恰好已到原计划时间.设汽车载人速度、空载时的速度、学生步行速度分别是匀速的,汽车离开学校的路程s(千米)与汽车行驶时间t(分钟)之间的函数关系如图,假设学生上下车时间忽略不计.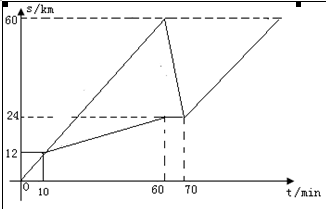
(1)原计划从学校出发到达博物馆的时间是 ▲ 分钟;
(2)求汽车在回头接第二批学生途中的速度;
(3)假设学生在步行途中不休息且步行速度每分钟减小0.04km,汽车载人时和空载时速度不变,问能否经过合理的安排,使得学生从学校出发全部到达目的地的时间比原计划时间早10分钟?如果能,请简要说出方案,并通过计算说明;如果不能,简要说明理由.
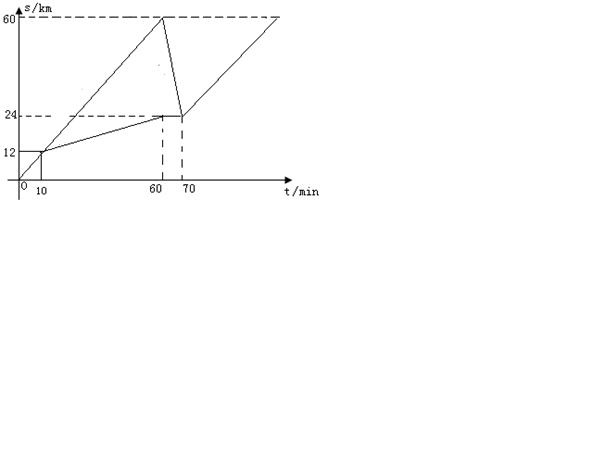
已知:如图,⊙O为 的外接圆,
的外接圆,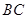 为⊙O的直径,作射线
为⊙O的直径,作射线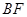 ,使得
,使得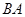 平分
平分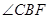 ,过点
,过点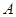 作
作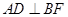 于点
于点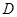 .
.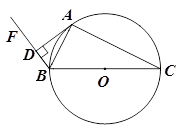
(1)求证:
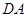 为⊙O的切线;
为⊙O的切线;(2)若
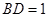 ,
,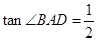 ,求⊙O的半径.
,求⊙O的半径.