P点为抛物线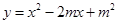 (
(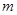 为常数,
为常数,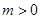 )上任一点,将抛物线绕顶点
)上任一点,将抛物线绕顶点 逆时针旋转
逆时针旋转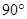 后得到的新图象与
后得到的新图象与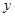 轴交于
轴交于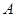 、
、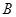 两点(点
两点(点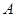 在点
在点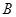 的上方),点
的上方),点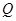 为点
为点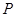 旋转后的对应点.
旋转后的对应点.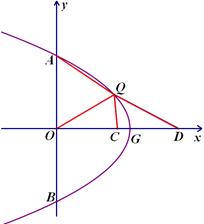
(1)当
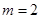 ,点
,点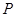 横坐标为4时,求
横坐标为4时,求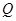 点的坐标;
点的坐标;(2)设点
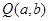 ,用含
,用含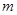 、
、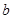 的代数式表示
的代数式表示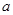 ;
;(3) 如图,点
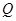 在第一象限内, 点
在第一象限内, 点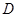 在
在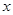 轴的正半轴上,点
轴的正半轴上,点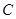 为
为 的中点,
的中点,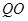 平分
平分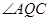 ,
,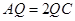 ,当
,当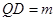 时,求
时,求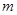 的值.
的值.
我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题:
(1)数轴上点A、点B分别是数﹣1、3对应的点,则点A与点B之间的距离为 .
(2)再选几个点试试,猜想:若点A、点B分别是数a、b对应的点,则点A与点B之间的距离为 .
(3)若数轴上点A对应的数为a,且|a﹣2|+|a﹣1|=12,且点A对应的数为 .
(4)继续利用绝对值的几何意义,探索|x﹣12|+|x+5|的最小值是 .
(5)已知数x,y满足|x+7|+|1﹣x|=19﹣|y﹣10|﹣|1+y|,则x+y的最小值是 ,最大值是 .
已知关于x的方程2x=x+m﹣3和关于y的方程3y﹣2(n﹣1)2=m,试思考:
(1)请用含m的代数式表示方程2x=x+m﹣3的解;
(2)若n=2,且上述两个方程的解互为相反数时,求m的值;
(3)若m=6,n=2时,设方程2x=x+m﹣3的解为x=a,方程3y﹣2(n﹣1)2=m的解为y=b,请比较3b﹣a与2的大小关系,并说明理由.
已知一次函数y=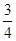 x+3的图象与x轴、y轴分别交于A、B两点,以线段AB为直角边在第二象限内作等腰直角三角形ABC,∠BAC=90°,如图1所示:
x+3的图象与x轴、y轴分别交于A、B两点,以线段AB为直角边在第二象限内作等腰直角三角形ABC,∠BAC=90°,如图1所示: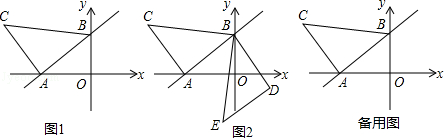
(1)填空:AB= ,BC= ;
(2)将△ABC绕点B逆时针旋转,①当AC与x轴平行时,则点A的坐标是 .
②当旋转角为90°时,得到△BDE,如图2所示,求过B、D两点直线的函数关系式.
③在②的条件,旋转过程中AC扫过的图形的面积是多少?
(3)将△ABC向右平移到△A′B′C′的位置,点C′为直线AB上的一点,请直接写出△ABC扫过的图形的面积.
为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离s甲是车速v的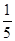 ,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
| 车速v(km/h) |
40 |
50 |
| 刹车距离s乙(m) |
12 |
17.5 |
(1)分别求出s甲、s乙与车速v的函数关系式;
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
如图1,AB是⊙O的直径,点C在⊙O上,且点C为弧BE的中点,连接AE并延长交BC延长线于点D.
(1)判断△ABD的形状,并说明理由;
(2)过点C作CM⊥AD,垂足为点F,如图2.
①求证:CF是⊙O的切线;
②若⊙O的半径为3,DF=1,求sinB的值.