发现规律（1）如图①，ΔABC与ΔADE都是等边三角形，直线-优题课

发现规律

（1）如图①， $ΔABC$ 与 $ΔADE$ 都是等边三角形，直线 $BD$ ， $CE$ 交于点 $F$ ．直线 $BD$ ， $AC$ 交于点 $H$ ．求 $∠ BFC$ 的度数．

（2）已知： $ΔABC$ 与 $ΔADE$ 的位置如图②所示，直线 $BD$ ， $CE$ 交于点 $F$ ．直线 $BD$ ， $AC$ 交于点 $H$ ．若 $∠ ABC = ∠ ADE = α$ ， $∠ ACB = ∠ AED = β$ ，求 $∠ BFC$ 的度数．

应用结论

（3）如图③，在平面直角坐标系中，点 $O$ 的坐标为 $(0, 0)$ ，点 $M$ 的坐标为 $(3, 0)$ ， $N$ 为 $y$ 轴上一动点，连接 $MN$ ．将线段 $MN$ 绕点 $M$ 逆时针旋转 $60 °$ 得到线段 $MK$ ，连接 $NK$ ， $OK$ ．求线段 $OK$ 长度的最小值．

科目数学题型解答题难度较难

知识点：旋转的性质垂线段最短三角形内角和定理相似三角形的判定与性质全等三角形的判定与性质等边三角形的判定与性质

如图， $AB$ 是 $⊙ O$ 的弦， $C$ 是 $⊙ O$ 外一点， $OC ⊥ OA$ ， $CO$ 交 $AB$ 于点 $P$ ，交 $⊙ O$ 于点 $D$ ，且 $CP = CB$ ．

（1）判断直线 $BC$ 与 $⊙ O$ 的位置关系，并说明理由；

（2）若 $∠ A = 30 °$ ， $OP = 1$ ，求图中阴影部分的面积．

甲、乙两地的路程为290千米，一辆汽车早上 $8 : 00$ 从甲地出发，匀速向乙地行驶，途中休息一段时间后．按原速继续前进，当离甲地路程为240千米时接到通知，要求中午 $12 : 00$ 准时到达乙地．设汽车出发 $x$ 小时后离甲地的路程为 $y$ 千米，图中折线 $OCDE$ 表示接到通知前 $y$ 与 $x$ 之间的函数关系．

（1）根据图象可知，休息前汽车行驶的速度为　　千米 $/$ 小时；

（2）求线段 $DE$ 所表示的 $y$ 与 $x$ 之间的函数表达式；

（3）接到通知后，汽车仍按原速行驶能否准时到达？请说明理由．

如图，三条笔直公路两两相交，交点分别为 $A$ 、 $B$ 、 $C$ ，测得 $∠ CAB = 30 °$ ， $∠ ABC = 45 °$ ， $AC = 8$ 千米，求 $A$ 、 $B$ 两点间的距离．（参考数据： $\sqrt{2} \approx 1.4$ ， $\sqrt{3} \approx 1.7$ ，结果精确到1千米）．

一只不透明的袋子中，装有三个大小、质地都相同的乒乓球，球面上分别标有字母 $A$ 、 $O$ 、 $K$ ．搅匀后先从袋中任意摸出一个球，将对应字母记入图中的左边方格内；然后将球放回袋中搅匀，再从袋中任意摸出一个球，将对应字母记入图中的右边方格内．

（1）第一次摸到字母 $A$ 的概率为　　；

（2）用画树状图或列表等方法求两个方格中的字母从左往右恰好组成“ $OK$ ”的概率．

为了响应市政府创建文明城市的号召，某校调查学生对市“文明公约十二条”的内容了解情况，随机抽取部分学生进行问卷调查，问卷共设置“非常了解”、“比较了解”、“一般了解”、“不了解”四个选项，分别记为 $A$ 、 $B$ 、 $C$ 、 $D$ ，根据调查结果绘制了如图尚不完整的统计图．

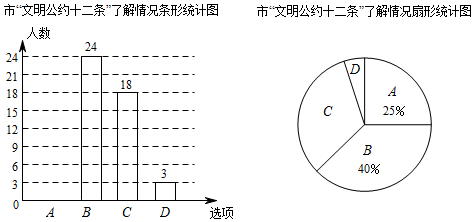
请解答下列问题：

（1）本次问卷共随机调查了　　学生，扇形统计图中 $C$ 选项对应的圆心角为　　度；

（2）请补全条形统计图；

（3）若该校有1200名学生，试估计该校选择“不了解”的学生有多少人？

试卷网试题网古诗词网作文网范文网