欧拉 ,1707年 年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数 、棱数 、面数 之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 |
三棱锥 |
三棱柱 |
正方体 |
正八面体 |
图形 |
|
|
|
|
顶点数 |
4 |
6 |
8 |
6 |
棱数 |
6 |
|
12 |
|
面数 |
4 |
5 |
|
8 |
(2)分析表中的数据,你能发现 、 、 之间有什么关系吗?请写出关系式: .
如图,在□ ABCD中,BD为对角线,EF垂直平分BD分别交AD、BC的于点E、F,交BD于点O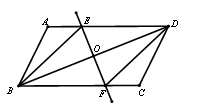
(1)试说明:BF=DE;
(2)试说明:△ABE≌△CDF;
(3)如果在□ ABCD中, AB=5,AD=10,有两动点P、Q分别从B、D两点同时出发,沿△BAE和△DFC各边运动一周,即点 自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图)
自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图)
如图: 在梯形ABCD中,AB∥DC,AD=DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB,垂足为F.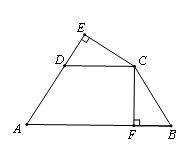
(1) 写出图中相等的线段; (已知的相等线段除外)
(2) 若AD=5,CF=4,求四边形ABCD的面积.
已知:如图,在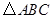 中,
中,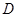 是
是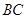 边的中点,
边的中点,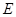 是
是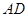 的中点,连接
的中点,连接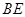 并延长到点
并延长到点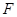 ,使EF=BE,连结AF、
,使EF=BE,连结AF、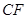 .
.
(1)试说明ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形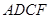 是矩形,并说明你的理由.
是矩形,并说明你的理由.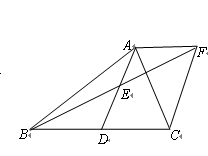
如图,等边三角形ABC,点E是AB上一点,点D在CB的延长线上,且ED=EC,
EF∥AC交BC于点F.
(1)试说明四边形AEFC是等腰梯形;
(2)请判断AE与DB的数量关系,并说明你的理由.
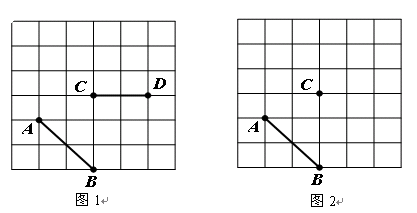
如图,正方形网格中,小格的顶点叫做格点,连接任意两个格点的线段叫做格点线段。
(1)如图1,格点线段AB、CD,请添加一条格点线段EF,使它们构成轴对称图形;
(2)如图2,格点线段AB和格点C,在网格中找一格点D,使格点A、B、C、D四点构成中心对称图形;
(3)在(2)的条件下,如果每一小正方形边长为1,那么四边形ABCD的面积S为_________.
(请直接填写)