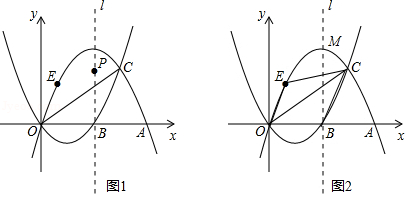
如图,在直角坐标系中,四边形 是平行四边形,经过 , , 三点的抛物线 与 轴的另一个交点为 ,其顶点为 ,对称轴与 轴交于点 .
(1)求这条抛物线对应的函数表达式;
(2)已知 是抛物线上的点,使得 的面积是 的面积的 ,求点 的坐标;
(3)已知 是抛物线对称轴上的点,满足在直线 上存在唯一的点 ,使得 ,求点 的坐标.

如图,若要在宽 为20米的城南大道两边安装路灯,路灯的灯臂 长2米,且与灯柱 成 角,路灯采用圆锥形灯罩,灯罩的轴线 与灯臂 垂直,当灯罩的轴线 通过公路路面的中心线时照明效果最好,此时,路灯的灯柱 高应该设计为多少米(结果保留根号)?

如图,在边长为1的正方形网格中建立平面直角坐标系,已知 三个顶点分别为 、 、 .
(1)画出 关于 轴对称的△ ;
(2)以原点 为位似中心,在 轴的上方画出△ ,使△ 与 位似,且位似比为2,并求出△ 的面积.

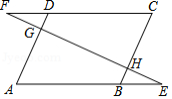
如右图,在 中, 、 分别是 、 延长线上的点,且 ,连接 交 、 于点 、 .求证: .
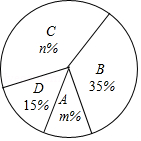
今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为 , , , 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
|
等级 |
成绩 |
频数(人数) |
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
6 |
根据以上信息,解答以下问题:
(1)表中的 ;
(2)扇形统计图中 , , 等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得 等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用 , 表示)和两名女生(用 , 表示),请用列表或画树状图的方法求恰好选取的是 和 的概率.
如图1,抛物线 与 相交于点 、 , 与 分别交 轴于点 、 ,且 为线段 的中点.
(1)求 的值;
(2)若 ,求 的面积;
(3)抛物线 的对称轴为 ,顶点为 ,在(2)的条件下:
①点 为抛物线 对称轴 上一动点,当 的周长最小时,求点 的坐标;
②如图2,点 在抛物线 上点 与点 之间运动,四边形 的面积是否存在最大值?若存在,求出面积的最大值和点 的坐标;若不存在,请说明理由.