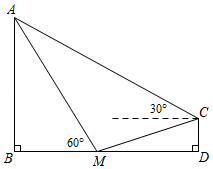
如图是把一个装有货物的长方体形状的木箱沿着坡面装进汽车货厢的示意图.已知汽车货厢高度米,货厢底面距地面的高度米,坡面与地面的夹角,木箱的长为2米,高和宽都是1.6米.通过计算判断:当,木箱底部顶点与坡面底部点重合时,木箱上部顶点会不会触碰到汽车货厢顶部.

我市某校准备成立四个活动小组: .声乐, .体育, .舞蹈, .书画,为了解学生对四个活动小组的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中必须选择而且只能选择一个小组,根据调查结果绘制如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次抽样调查共抽查了 名学生,扇形统计图中的 值是 ;
(2)请补全条形统计图;
(3)喜爱“书画”的学生中有两名男生和两名女生表现特别优秀,现从这4人中随机选取两人参加比赛,请用列表或画树状图的方法求出所选的两人恰好是一名男生和一名女生的概率.
如图1,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与 轴交于 点,抛物线 经过 , 两点,在第一象限的抛物线上取一点 ,过点 作 轴于点 ,交直线 于点 .
(1)求抛物线的函数表达式;
(2)是否存在点 ,使得 和 相似?若存在,请求出点 的坐标,若不存在,请说明理由;
(3)如图2, 是第一象限内抛物线上的动点(不与点 重合),点 是线段 上的动点.连接 , ,当四边形 是平行四边形且周长最大时,请直接写出点 的坐标.

已知,在 中, , 是 边上一点,连接 ,分别以 和 为直角边作 和 ,使 ,点 , 在 下方,连接 .
(1)如图1,当 , , 时,
求证:① ,② ;
(2)如图2,当 , , 时,猜想 和 之间的数量关系?并说明理由.

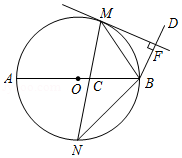
如图, , 是以 为直径的 上的点,且 ,弦 交 于点 , 平分 , 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
如图,某学校体育场看台的顶端 到地面的垂直距离 为 ,看台所在斜坡 的坡比 ,在点 处测得旗杆顶点 的仰角为 ,在点 处测得旗杆顶点 的仰角为 ,且 , , 三点在同一水平线上,求旗杆 的高度.(结果精确到 ,参考数据: ,