某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记 表示2台机器三年内共需更换的易损零件数, 表示购买2台机器的同时购买的易损零件数.
(Ⅰ)求 的分布列;
(Ⅱ)若要求 ,确定 的最小值;
(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在 与 之中选其一,应选用哪个?

(本小题满分12分)
已知等差数列 的首项
的首项 公差
公差 且第二项、第五项、第十四项分别是等比数列
且第二项、第五项、第十四项分别是等比数列 的第二项、第三项、第四项。
的第二项、第三项、第四项。
(1)求数列 与数列
与数列 的通项公式;
的通项公式;
(2)设数列 对任意正整数
对任意正整数 均有
均有 成立,
成立,
(3)求数列 的前
的前 项和
项和
(本小题满分12分)
某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作。比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。
假设每个运动员完成每个系列中的K和D两个动作的得分是相互独立的。根据赛前训练的统计数据,某运动员完成甲系列和乙系列中的K和D两个动作的情况如下表:
表1:甲系列表2:乙系列
| 动作 |
K动作 |
D动作 |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
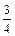 |
 |
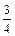 |
 |
| 动作 |
K动作 |
D动作 |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
 |
 |
 |
 |
现该运动员最后一个出场,之前其他运动员的最高得分为115分。
(1)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由。
并求其获得第一名的概率。
(2)若该运动员选择乙系列,求其成绩 的分布列及数学期望
的分布列及数学期望
(本小题满分12分)
已知函数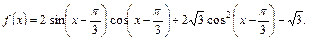
(1)求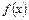 的单调递增区间;
的单调递增区间;
(2)求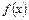 的最大值及取得最大值时相应的
的最大值及取得最大值时相应的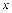 的值。
的值。
(本小题满分12分)
已知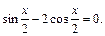
(1)求 的值;
的值;
(2)求 的值。
的值。
已知函数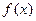 的定义域为[0,1]且同时满足:①对任意
的定义域为[0,1]且同时满足:①对任意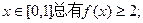 ②
②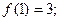 ③若
③若
(I)求 的值;
的值;
(II)求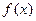 的最大值;
的最大值;
(III)设数列 的前n项和为Sn,且
的前n项和为Sn,且 ,
,
求: