设圆 的圆心为 ,直线 过点 且与 轴不重合, 交圆 于 , 两点,过 作 的平行线交 于点 .
(Ⅰ)证明 为定值,并写出点 的轨迹方程;
(Ⅱ)设点 的轨迹为曲线 ,直线 交 于 , 两点,过 且与 垂直的直线与圆 交于 , 两点,求四边形 面积的取值范围.
已知数列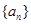 中,
中,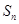 是
是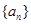 的前
的前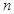 项和,且
项和,且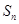 是
是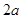 与
与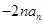 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数.
(1)求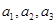 ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.
设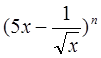 的展开式的各项系数之和为
的展开式的各项系数之和为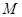 ,二项式系数之和为
,二项式系数之和为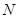 ,
,
若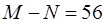 ,(1) 求 n,N,M(2)求展开式中常数项为.
,(1) 求 n,N,M(2)求展开式中常数项为.
用数字0,1,2,3,4,5组成没有重复数字的数.
求:(1)可以组成多少个四位数?
(2)可以组成多少个不同的四位偶数?
(3)可以组成多少个能被5整除的四位数?
已知复数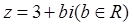 ,且
,且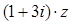 为纯虚数.
为纯虚数.
(1)求复数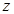 ;(2)若
;(2)若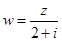 ,求复数
,求复数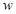 的模
的模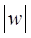
若有穷数列 (
(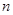 是正整数),满足
是正整数),满足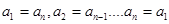 即
即 (
(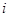 是正整数,且
是正整数,且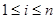 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列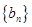 是项数为7的对称数列,且
是项数为7的对称数列,且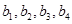 成等差数列,
成等差数列,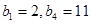 ,试写出
,试写出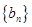 的每一项
的每一项
(2)已知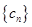 是项数为
是项数为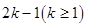 的对称数列,且
的对称数列,且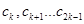 构成首项为50,公差为
构成首项为50,公差为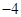 的等差数列,数列
的等差数列,数列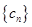 的前
的前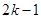 项和为
项和为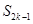 ,则当
,则当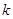 为何值时,
为何值时,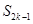 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数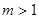 ,试写出所有项数不超过
,试写出所有项数不超过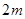 的对称数列,使得
的对称数列,使得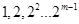 成为数列中的连续项;当
成为数列中的连续项;当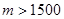 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和