若无穷数列 满足:只要 ,必有 ,则称 具有性质 .
(1)若 具有性质 ,且 , , , , ,求 ;
(2)若无穷数列 是等差数列,无穷数列 是公比为正数的等比数列, ; , ,判断 是否具有性质 ,并说明理由;
(3)设 是无穷数列,已知 ,求证:“对任意 , 都具有性质 ”的充要条件为“ 是常数列”.
已知函数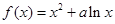 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为 .
.
(Ⅰ)求实数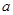 的值;
的值;
(Ⅱ)判断方程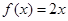 根的个数,证明你的结论;
根的个数,证明你的结论;
(Ⅲ)探究:是否存在这样的点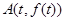 ,使得曲线
,使得曲线 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
平面内动点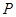 到点
到点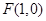 的距离等于它到直线
的距离等于它到直线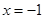 的距离,记点
的距离,记点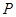 的轨迹为曲
的轨迹为曲 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若点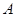 ,
,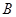 ,
,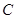 是
是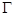 上的不同三点,且满足
上的不同三点,且满足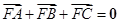 .证明:
.证明:  不可能为直角三角形.
不可能为直角三角形.
2013年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 |
PM2.5浓度 (微克/立方米) |
频数(天) |
频率 |
| 第一组 |
(0,25] |
5 |
0.25 |
| 第二组 |
(25,50] |
10 |
0.5 |
| 第三组 |
(50,75] |
3 |
0.15 |
| 第四组 |
(75,100) |
2 |
0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------①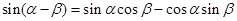 ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: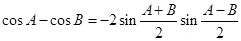 ;
;
(Ⅱ)若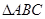 的三个内角
的三个内角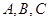 满足
满足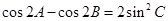 ,试判断
,试判断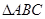 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
在直角梯形ABCD中,AD//BC,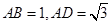 ,
,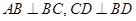 ,如图(1).把
,如图(1).把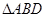 沿
沿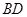 翻折,使得平面
翻折,使得平面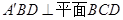 ,如图(2).
,如图(2).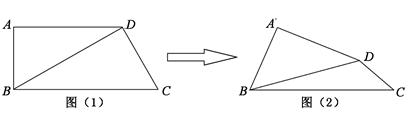
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥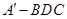 的体积;
的体积;
(Ⅲ)在线段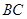 上是否存在点N,使得
上是否存在点N,使得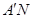
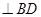 ?若存在,请求出
?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.