选修4-5:不等式选讲
已知 ,求证:
,求证:
(1) ;
;
(2) .
.
(本小题满分12分)一射击测试每人射击三次,每击中目标一次记10分。没有击中记0分,某人每次击中目标的概率为
(I)求此人得20分的概率;(I I)求此人得分的数学期望与方差。
I)求此人得分的数学期望与方差。
(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个白球,乙盒内有大小相同的2个红球和4个白球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为白球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
如图,四棱锥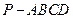 中,
中,
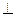 底面
底面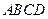 ,
, 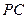
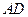 .底面
.底面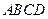 为梯形,
为梯形,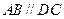 ,
,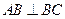 .
. ,点
,点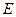 在棱
在棱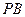 上,且
上,且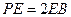 .
.
(1)求证: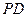
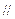
 平面
平面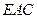 ;
;
(2)求二面角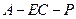 的大小.
的大小.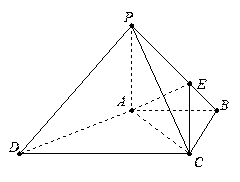
(本小题满分12分)
已知圆 的方程为
的方程为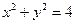 .
.
(1)求过点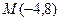 的圆
的圆 的切线方程;
的切线方程;
(2)过点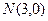 作直线与圆
作直线与圆 交于
交于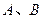 两点,求
两点,求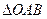 的最大面积以及此时直线
的最大面积以及此时直线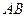 的斜率.
的斜率.
(本小题满分12分)
已知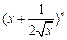 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值; (2)求展开式中系数最大的项.
(2)求展开式中系数最大的项.