如图，在正方形 中， ， 为边 上的两个三等分点，点 关于 的对称点为 ， 的延长线交 于点 ．
（1）求证： ；
（2）求 的大小；
（3）求证： ．
提出问题
如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．
类比探究
如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．
拓展延伸
如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．
如图，某文化广场灯柱AB被钢缆CD固定，已知CB＝5米，且sin∠DCB=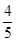
．
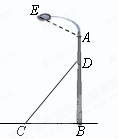
（1）求钢缆CD的长度；
（2）若AD＝2米，灯的顶端E距离A处1.6米，且∠EAB＝120°，则灯的顶端E距离地面多少米？
如图，一次函数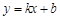
与反比例函数
的图象交于A（2，1），B（-1，
）两点．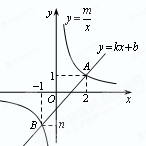
（1）求m、k、b的值；
（2）连接OA、OB，计算三角形OAB的面积；
（3）结合图象直接写出不等式
的解集．
在某项针对18～35岁的青年人每天发微博数量的调查中，设一个人的“日均发微博条数”为m，规定：当m≥10时为A级，当5≤m＜10时为B级，当0≤m＜5时为C级．现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查，所抽青年人的“日均发微博条数”的数据如下：
（1）求样本数据中为A级的频率；
（2）试估计1000个18～35岁的青年人中“日均发微博条数”为A级的人数；
（3）从样本数据为C级的人中随机抽取2人，用列举法求抽得2个人的“日均发微博条数”都是3的概率．
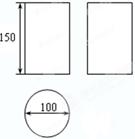
某工厂要加工一批茶叶罐，设计者给出了茶叶罐的三视图，如图10，请你按照三视图确定制作每个密封罐所需钢板的面积．（单位：毫米）