疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 （万人）与各自接种时间 （天 之间的关系如图所示．
（1）直接写出乙地每天接种的人数及 的值；
（2）当甲地接种速度放缓后，求 关于 的函数解析式，并写出自变量 的取值范围；
（3）当乙地完成接种任务时，求甲地未接种疫苗的人数．
对于边长为2的正△ABC，建立适当的直角坐标系，写出各个顶点的坐标．
如图，抛物线y=
x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（-1，0）．
⑴ 求抛物线的解析式及顶点D的坐标；
⑵ 判断△ABC的形状，证明你的结论；
⑶ 点M(m，0)是x轴上的一个动点，当CM+DM的值最小时，求m的值．
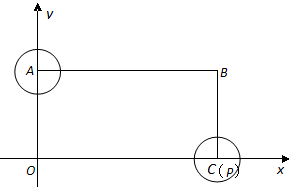
如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．
（1）在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的
；
（2）在点P的运动过程中，是否存在某一时刻，⊙A与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．