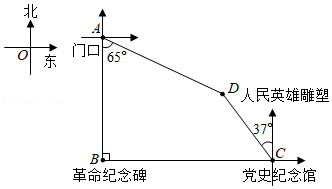
时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口 处向正南方向走300米到达革命纪念碑 处,再从 处向正东方向走到党史纪念馆 处,然后从 处向北偏西 方向走200米到达人民英雄雕塑 处,最后从 处回到 处.已知人民英雄雕塑在基地门口的南偏东 方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据: , , , , ,
某中学的地理兴趣小组在本校学生中开展主题为“地震知识知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表: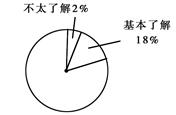
| 等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
| 频数 |
40 |
120 |
n |
4 |
| 频率 |
0.2 |
m |
0.18 |
0.02 |
(1)表中的m的值为_______,n的值为.
(2)根据表中的数据,请你计算“非常了解”的频率在下图中所对应的扇形的圆心角的度数,并补全扇形统计图.
(3)若该校有1500名学生,请根据调查结果估计这些学生中“比较了解”的人数约为多少?
如图,在平行四边形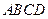 中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
(1)求证: ∠BAE=∠DAF;
∠BAE=∠DAF;
(2)若AE=4,AF=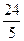 ,
,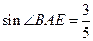 ,求CF的长.
,求CF的长.
随着人们节能意识的增强,节能产品进入千家万户,今年1月小明家将天燃气热水器换成了太阳能热水器.去年12月份小明家的燃气费是96元,从今年1月份起天燃气价格每立方米上涨25%,小明家2月份的用气量比去年12月份少10立方米,2月份的燃气费是90元.问小明家2月份用气多少立方米.
如图,在四边形ABCD中, AC是∠DAE的平分线,DA∥CE,∠AEB=∠CEB. 求证:AB="CB." 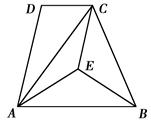
先化简,再求值: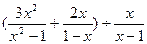 ,其中
,其中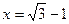 .
.