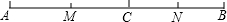如图,抛物线 经过点 , ,与 轴正半轴交于点 ,且 ,抛物线的顶点为 ,对称轴交 轴于点 .直线 经过 , 两点.
(1)求抛物线及直线 的函数表达式;
(2)点 是抛物线对称轴上一点,当 的值最小时,求出点 的坐标及 的最小值;
(3)连接 ,若点 是抛物线上对称轴右侧一点,点 是直线 上一点,试探究是否存在以点 为直角顶点的 ,且满足 .若存在,求出点 的坐标;若不存在,请说明理由.

已知∠AOB=50°,如果以∠AOB的顶点O为端点引射线OC,使∠AOC:∠BOC=3:2,试求∠AOC的度数.
(1)如图所示,将一副三角尺的直角顶点重合在点O处.
①∠AOD和∠BOC相等吗?说明理由.
②∠AOC和∠BOD在数量上有何关系?试写一个关系式.
(2)如图,已知线段AB=6,延长线段AB到C,使BC=2AB,点D是AC的中点,
求①AC的长;②BD的长.

如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠BOC=40°,求∠EOD的度数.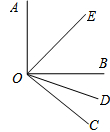
如图,已知∠AOE=140°,∠COD=30°,OB是∠AOC的平分线,OD是∠COE的平分线,求∠AOB的度数.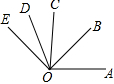
如图,点C在线段AB上,AC="8" cm,CB="6" cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB="a" cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC-BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?