问题提出
(1)如图1,在 中, , , , 是 的中点,点 在 上,且 ,求四边形 的面积.(结果保留根号)
问题解决
(2)某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上规划一个五边形河畔公园 .按设计要求,要在五边形河畔公园 内挖一个四边形人工湖 ,使点 、 、 、 分别在边 、 、 、 上,且满足 , .已知五边形 中, , , , , .为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形 面积的最小值及这时点 到点 的距离;若不存在,请说明理由.

如图,在等腰梯形 中,
中,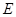 为底
为底 的中点,连结
的中点,连结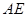 、
、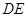 .
.
求证: .
.
已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交?
如图,用长为32米的篱笆围成一个外形为矩形的花圃,花圃的一边利用原有墙,中间用2道篱笆割成3个小矩形.已知原有墙的最大可利用长度为15米,花圃的面积为S平方米,平行于原有墙的一边BC长为x米.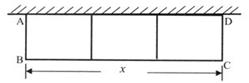
(1)求S关于x的函数关系式;
(2)当围成的花圃面积为60平方米时,求AB的长;
(3)能否围成面积比60平方米更大的花圃?如果能,那么最大的面积是多少?如果不能,请说明理由.
如图,正比例函数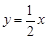 的图象与反比例函数
的图象与反比例函数 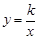
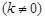 在第一象限的图象交于
在第一象限的图象交于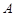 点,过
点,过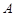 点作
点作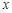 轴的垂线,垂足为
轴的垂线,垂足为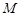 ,已知
,已知 的面积为1.
的面积为1.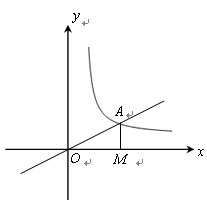
(1)求反比例函数的解析式;
(2)当x>0时,根据图象直接写出不等式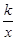 >
>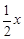 的解;
的解;
(3)如果 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 与点
与点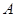 不重合),且
不重合),且 点的横坐标为1,在
点的横坐标为1,在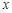 轴上求一点
轴上求一点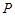 ,使
,使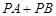 最小.
最小.
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.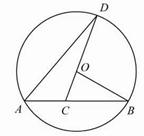
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.