如图1，在平面直角坐标系中，抛物线与 轴分别交于 、 两点，与 轴交于点 ，抛物线的顶点坐标为 ，连结 、 、 ．
（1）求抛物线的表达式；
（2）判断 的形状，并说明理由；
（3）如图2，以 为圆心， 为半径作 ，在 上是否存在点 ，使得 的值最小，若存在，请求出最小值；若不存在，请说明理由．
如图，在△ABC中，MN∥BD交AC于点P， 
的平分线分别交MN于点E，F。
（1）求证：PE=PF
（2）当MN与AC的交点P在什么位置时，四边形AECF是矩形，请说明理由；
（3）当△ABC满足什么条件时，四边形AECF是正方形（不需证明）
如图，直线AB与x轴交于点A（1，0），与y 轴交于点B（0，-2）。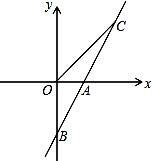
（1）求直线AB的解析式。
（2）若直线AB上的点C在第一象限，且S△BOC="2" ，求点C的坐标。
某商场服装部为了调动营业员的积极性，决定实行目标管理，即确定一个月销售目标，根据目标完成的情况对营业员进行适当的奖惩，为了确定一个适当的目标，商场统计了每个营业员在某月的销售额（万元）如下图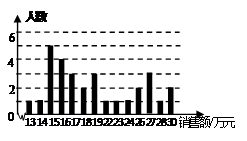
（1）求平均的月销售额及数据的中位数和众数
（2）如果想确定一个较高的销售目标，你认为月销售额定为多少合适？说明理由。
如图，在四边形ABCD中，AB
BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积．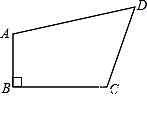
已知反比例函数y1=
的图象与一次函数y2=ax+b的图象交于点A（1，4）和点B（m，﹣2），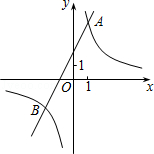
（1）求这两个函数的关系式；
（2）观察图象，写出使得y1＞y2成立的自变量x的取值范围；
（3）若P为Y轴上得一点，连接PA、PB，△PAB的面积为6，求P点的坐标。