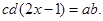抛物线 与 轴交于 、 两点,与 轴交于点 ,且 , .

(1)求抛物线的解析式;
(2)如图1,点 是抛物线上位于直线 上方的一点, 与 相交于点 ,当 时,求点 的坐标;
(3)如图2,点 是抛物线的顶点,将抛物线沿 方向平移,使点 落在点 处,且 ,点 是平移后所得抛物线上位于 左侧的一点, 轴交直线 于点 ,连结 .当 的值最小时,求 的长.
计算:
如图,从左到右,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所有整数之和都相等。
(I)可求得
 ,第
,第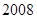 个格子中的数为__________;
个格子中的数为__________;(II)判断:前
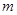 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为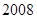 ?若能,求出
?若能,求出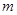 的值;若不能,请说明理由;
的值;若不能,请说明理由;(III)如果
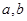 为前三个格子中的任意两个数,那么所有的
为前三个格子中的任意两个数,那么所有的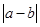 的和可以通过计算|
的和可以通过计算|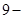 ★|+|
★|+|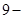 ☆|+|★
☆|+|★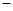 ☆|+|★
☆|+|★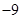 |+|☆
|+|☆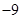 |+|☆
|+|☆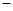 ★|得到,若
★|得到,若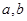 为前
为前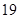 个格子中的任意两个数,则所有的
个格子中的任意两个数,则所有的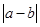 的和为__________.
的和为__________.
计算:
王明在计算一个多项式减去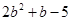 的差时,因一时疏忽忘了对两个多项式用括号括起来,因此减式后面两项没有变号,结果得到的差是
的差时,因一时疏忽忘了对两个多项式用括号括起来,因此减式后面两项没有变号,结果得到的差是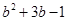 。据此你能求出这个多项式并算出正确的结果吗?
。据此你能求出这个多项式并算出正确的结果吗?
解方程:(I)
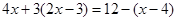
(II)
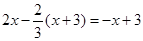
(III)

先化简再求值:(I) 求
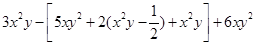 的值,其中
的值,其中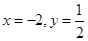
(II) 已知
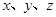 满足:⑴已知
满足:⑴已知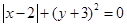 ,⑵
,⑵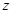 是最大的负整数,化简求值:
是最大的负整数,化简求值: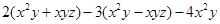
已知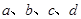 是四个互不相等的整数,且它们的积
是四个互不相等的整数,且它们的积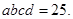
⑴ 求
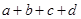 的值;
的值;⑵ 解关于
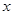 的方程:
的方程: