△ABC的内角A,B,C的对边分别为a,b,c,已知 .
(1)求A;
(2)若 ,证明:△ABC是直角三角形.
设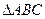 中的内角
中的内角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, ,且
,且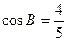 ,
, .
.
(Ⅰ)当 时,求角
时,求角 的度数;(Ⅱ)求
的度数;(Ⅱ)求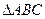 面积的最大值.
面积的最大值.
函数 ,
,
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)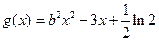 ,当
,当 ,
, 时,
时,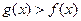 恒有解,求
恒有解,求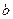 的取值范围.
的取值范围.
设数列{an}为前n项和为Sn,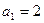 ,数列{ Sn +2}是以2为公比的等比数列.
,数列{ Sn +2}是以2为公比的等比数列.
(1)求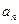 ;
;
(2)抽去数列{an}中的第1项,第4项,第7项,……,第3n-2项,余下的项顺序不变,组成一个新数列{cn},若{cn}的前n项和为Tn,求证:
<≤
如图(1), 是直径
是直径 的圆上一点,
的圆上一点,
 为圆O的切线,
为圆O的切线, 为切点,
为切点, 为等边三角形,连接
为等边三角形,连接 交
交 于
于 ,以
,以 为折痕将
为折痕将 翻折到图(2)所示
翻折到图(2)所示 的位置,点P为平面ABC外的点.
的位置,点P为平面ABC外的点.
(1)求证:异面直线 和
和 互相垂直;
互相垂直;
(2)若 为
为 上一点,且
上一点,且 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
在平面直角坐标系中,点 、
、 ,已知
,已知 ,
, 的垂直平分线
的垂直平分线 交
交 于
于 ,当点
,当点 为动点时,点
为动点时,点 的轨迹图形设为
的轨迹图形设为 .
.
(1)求 的标准方程;
的标准方程;
(2)点 为
为 上一动点,点
上一动点,点 为坐标原点,曲线
为坐标原点,曲线 的右焦点为
的右焦点为 ,求
,求 的最小值.
的最小值.