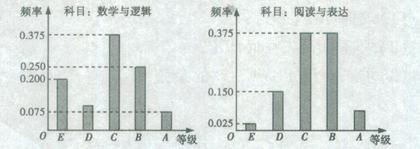
在三棱柱 ABC- A 1 B 1 C 1中, AB⊥ AC, B 1 C⊥平面 ABC, E, F分别是 AC, B 1 C的中点.

(1)求证: EF∥平面 AB 1 C 1;
(2)求证:平面 AB 1 C⊥平面 ABB 1.
设数列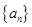 是公比大于1的等比数列,
是公比大于1的等比数列,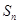 为数列
为数列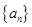 的前
的前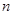 项和,已知
项和,已知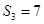 ,且
,且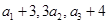 构成等差数列.
构成等差数列.
(1)求数列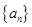 的通项公式;
的通项公式;
(2)令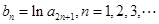 ,求数列
,求数列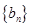 的前
的前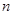 项的和
项的和 .
.
已知函数
(1)当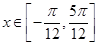 时,求函数
时,求函数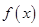 取得最大值和最小值;
取得最大值和最小值;
(2)设锐角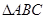 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是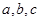 ,且
,且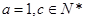 ,若向量
,若向量 与向量
与向量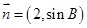 平行,求
平行,求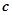 的值.
的值.
已知函数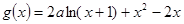 .
.
(1)当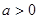 时,讨论函数
时,讨论函数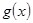 的单调性;
的单调性;
(2)当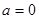 时,在函数
时,在函数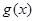 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为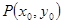 ,试探究函数
,试探究函数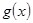 在Q
在Q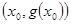 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?
(3)试判断当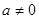 时
时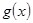 图象是否存在不同的两点A、B具有(2)问中所得出的结论.
图象是否存在不同的两点A、B具有(2)问中所得出的结论.
在平面直角坐标系中,长度为3的线段AB的端点A、B分别在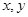 轴上滑动,点M在线段AB上,且
轴上滑动,点M在线段AB上,且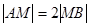 ,
,
(1)若点M的轨迹为曲线C,求其方程;
(2)过点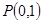 的直线
的直线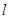 与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求
与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求 面积的最大值.
面积的最大值.
某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容,成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩等级为B的考生有10人
(1)求该班考生中“阅读与表达”科目中成绩等级为A的人数;
(2)若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分,该考场共10人得分大于7分,其中2人10分,2人9分,6人8分,从这10人中随机抽取2人,求2人成绩之和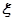 的分布列。
的分布列。