某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底 O在水平线 MN上、桥 AB与 MN平行, 为铅垂线( 在 AB上).经测量,左侧曲线 AO上任一点 D到 MN的距离 (米)与 D到 的距离 a(米)之间满足关系式 ;右侧曲线 BO上任一点 F到 MN的距离 (米)与 F到 的距离 b(米)之间满足关系式 .已知点 B到 的距离为40米.

(1)求桥 AB的长度;
(2)计划在谷底两侧建造平行于 的桥墩 CD和 EF,且 CE为80米,其中 C, E在 AB上(不包括端点).桥墩 EF每米造价 k(万元)、桥墩 CD每米造价 (万元)( k>0).问 为多少米时,桥墩 CD与 EF的总造价最低?
(本题满分12分如图,四边形 为矩形,且
为矩形,且 ,
, ,
, 为
为 上的动点。
上的动点。
(1) 当 为
为 的中点时,求证:
的中点时,求证: ;
;
(2) 设 ,在线段
,在线段 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角 的平面角大小为
的平面角大小为 。试确定点E的位置。
。试确定点E的位置。
一投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.经过多次试验,某人投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋。
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分 的数学期望
的数学期望 。
。
已知数列 中,
中, 且点
且点 在直线
在直线 上。
上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若函数 求函数
求函数 的最小值;
的最小值;
已知二次函数 对任意
对任意 ,都有
,都有 成立,设向量
成立,设向量 (sinx,2),
(sinx,2), (2sinx,
(2sinx, ),
), (cos2x,1),
(cos2x,1), (1,2),当
(1,2),当 [0,
[0, ]时,求不等式f(
]时,求不等式f( )>f(
)>f( )的解集.
)的解集.
.(本题满分14分)已知函数f(x)=sin(ωx+φ),其中ω>0,|φ|<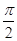 .
.
(1)若cos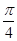 cosφ-sin
cosφ-sin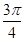 sinφ=0,求φ的值;
sinφ=0,求φ的值;
(2)在(1)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于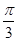 ,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.