(本题12分)如图,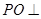 平面
平面 ,点
,点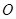 在
在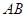 上,
上,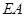 ∥
∥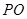 ,四边形
,四边形 为直角梯形,
为直角梯形,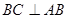 ,
,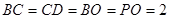 ,
,
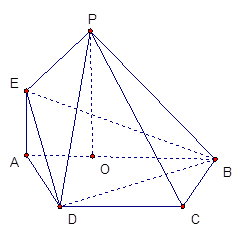
(1)求证: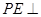 平面
平面 ;
;
(2)求二面角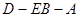 的余弦值;
的余弦值;
(3)直线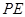 上是否存在点
上是否存在点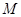 ,使
,使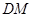 ∥平面
∥平面 ,若存在,求出点
,若存在,求出点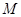 ;若不存在,说明理由。
;若不存在,说明理由。
数列 满足
满足 ,
, .(1)求
.(1)求 通项公式
通项公式 ;(2)令
;(2)令 ,数列
,数列 前
前 项和为
项和为 ,求证:当
,求证:当 时,
时, ;(3)证明:
;(3)证明: .
.
设数列{a }的首项a
}的首项a =1,前n项和S
=1,前n项和S 满足关系式:3tS
满足关系式:3tS -(2t+3)S
-(2t+3)S =3t(t>0,n=2,3,4…).(1)求证:数列{a
=3t(t>0,n=2,3,4…).(1)求证:数列{a }是等比数列;(2)设数列{a
}是等比数列;(2)设数列{a }的公比为f(t),若数列{b
}的公比为f(t),若数列{b }满足:b
}满足:b =1,b
=1,b =f(
=f( )(n=2,3,4…),求
)(n=2,3,4…),求
 ;(3) 对于(2)中的数列{b
;(3) 对于(2)中的数列{b },求b
},求b b
b -b
-b b
b +b
+b b
b -…+(-1)
-…+(-1) b
b b
b 的和。
的和。
已知函数 (1)求函数
(1)求函数 在区间[1,
在区间[1, ]上的最大值、最小值;
]上的最大值、最小值;
(2)求证:在区间(1, )上,函数
)上,函数 图象在函数
图象在函数 图象的下方;
图象的下方;
(3)设函数 ,求证:
,求证: ≥
≥ 。(
。( )
)
一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率;(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分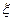 的概率分布列及数学期望。
的概率分布列及数学期望。
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人. 0(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.