在平面直角坐标系 xOy中,已知椭圆 的左、右焦点分别为 F 1, F 2,点 A在椭圆 E上且在第一象限内, AF 2⊥ F 1 F 2,直线 AF 1与椭圆 E相交于另一点 B.

(1)求△ AF 1 F 2的周长;
(2)在 x轴上任取一点 P,直线 AP与椭圆 E的右准线相交于点 Q,求 的最小值;
(3)设点 M在椭圆 E上,记△ OAB与△ MAB的面积分别为 S 1, S 2,若 S 2=3 S 1,求点 M的坐标.
已知函数f(x)=lnx+a ,其中a为大于零的常数.
,其中a为大于零的常数.
(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证:对于任意的n∈N*,且n>1时,都有lnn> +
+ +…+
+…+ 恒成立.
恒成立.
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如表:
| 时间(将第x天记为x)x |
1 |
10 |
11 |
18 |
| 单价(元/件)P |
9 |
0 |
1 |
8 |
而这20天相应的销售量Q(百件/天)与x对应的点(x,Q)在如图所示的半圆上.
(1)写出每天销售收入y(元)与时间x(天)的函数关系式y=f(x).
(2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价P定为多少元为好?(结果精确到1元)
若x,y满足约束条件
(1)求目标函数z= x-y+
x-y+ 的最值.
的最值.
(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.
已知函数f(x)=x2+2x+a.
(1)当a= 时,求不等式f(x)>1的解集.
时,求不等式f(x)>1的解集.
(2)若对于任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
已知a,b,c,d∈R,用分析法证明:ac+bd≤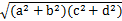 并指明等号何时成立.
并指明等号何时成立.