已知函数f(x)=lnx+a ,其中a为大于零的常数.
,其中a为大于零的常数.
(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证:对于任意的n∈N*,且n>1时,都有lnn> +
+ +…+
+…+ 恒成立.
恒成立.
(本小题13分)
金融风暴对全球经济产生了影响,温总理在广东省调研时强调:在当前的经济形势下,要大力扶持中小企业,使中小企业健康发展。为响应这一精神,某地方政府决定扶持一民营企业加大对A、B两种产品的生产。根据市场调查与预测,A产品的利润与投资成正比,其关系如图①,B产品的利润与投资的算术平方根成正比,其关系如图②(注:利润与投资单位:万元).
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元?(精确到1万元)
(本小题13分)
已知圆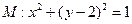 ,
, 是
是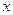 轴上的动点,
轴上的动点, 、
、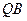 分别切圆
分别切圆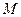 于
于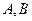 两点
两点
(1)若点 的坐标为(1,0),求切线
的坐标为(1,0),求切线 、
、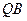 的方程
的方程
(2)求四边形 的面积的最小值
的面积的最小值
(3)若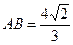 ,求直线
,求直线 的方程
的方程
(本小题12分)
如图,正方体ABCD—A1B1C1D1中,M、N分别为AB、BC的中点.
(Ⅰ)求证:平面B1MN⊥平面BB1D1D;
(II)当点P为棱DD1中点时,求直线MB1与平面A1C1P所成角的正弦值; 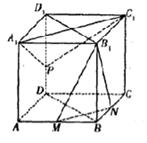
(本小题满分12分)
已知向量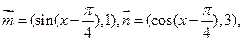
 。
。
(1)若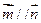 ,求
,求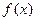 ;
;
(2)若函数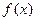 的图像向右平移
的图像向右平移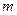 (
( )个单位长度,再向下平移3个单位后图像对应的函数
)个单位长度,再向下平移3个单位后图像对应的函数 是奇函数,求
是奇函数,求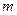 的最小值。
的最小值。
(本小题12分)
已知函数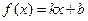 的图象过点
的图象过点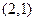 ,且方向向量
,且方向向量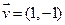 .
.
若不等式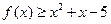 的解集为
的解集为 ,且
,且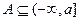 .
.
(1)求 的取值范围;(2)解关于
的取值范围;(2)解关于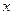 的不等式
的不等式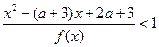 .
.