某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 |
[0,200] |
(200,400] |
(400,600] |
1(优) |
2 |
16 |
25 |
2(良) |
5 |
10 |
12 |
3(轻度污染) |
6 |
7 |
8 |
4(中度污染) |
7 |
2 |
0 |
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天"空气质量好";若某天的空气质量等级为3或4,则称这天"空气质量不好".根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 |
人次>400 |
|
空气质量好 |
||
空气质量不好 |
附: ,
P( K 2≥ k) |
0.050 |
0.010 |
0.001 |
k |
3.841 |
6.635 |
10.828 |
中央电视台星光大道某期节目中,有5位实力均等的选手参加比赛,经过四轮比赛决出周冠军(每一轮比赛淘汰l位选手).
(1)求甲、乙两位选手都进入第三轮比赛的概率;
(2)求甲选手在第三轮被淘汰的的概率.
已知数列 满足:
满足: ,其中
,其中 为数列
为数列 的前
的前 项和.
项和.
(1)试求 的通项公式;
的通项公式;
(2)若数列 满足:
满足: ,试求
,试求 的前
的前 项和
项和 .
.
在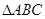 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为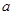 、
、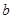 、
、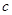 ,且
,且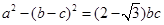 ,
, ,
,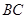 边上中线
边上中线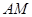 的长为
的长为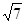 .
.
(1) 求角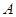 和角
和角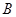 的大小;
的大小;
(2) 求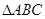 的面积.
的面积.
已知抛物线 ,直线
,直线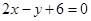 截抛物线C所得弦长为
截抛物线C所得弦长为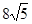 .
.
(1)求抛物线的方程;
(2)已知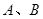 是抛物线上异于原点
是抛物线上异于原点 的两个动点,记
的两个动点,记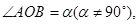 若
若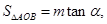 试求当
试求当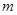 取得最小值时
取得最小值时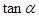 的最大值.
的最大值.
已知函数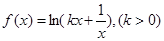 在
在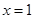 处取得极小值.
处取得极小值.
(1)求 的值;
的值;
(2)若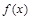 在
在 处的切线方程为
处的切线方程为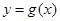 ,求证:当
,求证:当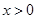 时,曲线
时,曲线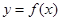 不可能在直线
不可能在直线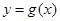 的下方.
的下方.