已知 是各项均为正数的等比数列, .
(1)求 的通项公式;
(2)设 ,求数列
的前n项和.
,求数列
的前n项和.
(本小题满分12分)
已知函数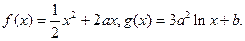
(Ⅰ)设两曲线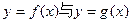 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若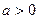 ,试建立
,试建立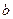 关于
关于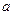 的函数关系式,并求
的函数关系式,并求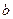 的最大值;
的最大值;
(Ⅱ)若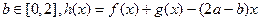 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求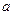 的取值范围。
的取值范围。
(本小题满分12分)
已知斜三棱柱ABC—A1B1C1,侧面ACC1A1与底面ABC垂直, ,BC=2,
,BC=2,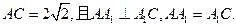
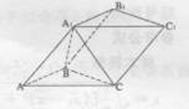
(Ⅰ)试判断A1A与平面A1BC是否垂直,并说明理由;
(Ⅱ)求底面ABC与侧面BB1C1C所成二面角的余弦值。
(本小题满分12分)
为征求个人所得税修改建议,某机构对不发居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在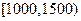 )
)
(I)求居民月收入在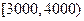 的频率;
的频率;
(II)根据频率分布直方图估算样本数据的中位数;
(III)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析,则月收入在 的这段应抽多少人?
的这段应抽多少人?
(本小题满分12分)
如图所示,甲船由A岛出发向北偏东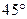 的方向作匀
的方向作匀 速直线航行,速度为
速直线航行,速度为 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东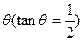 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为
 海里/小时。
海里/小时。
(1)若两船能相遇,求 。
。
(2)当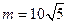 时,求两船出发后多长时间距离最近,最近距离为多少海里?
时,求两船出发后多长时间距离最近,最近距离为多少海里?
(求100~999中的水仙花数,所谓水仙花数是一个三位数,它的各位数字的立方和等于该数,例如153是一个水仙花数,因为 .试编一段程序,找出所有的水仙花数.
.试编一段程序,找出所有的水仙花数.