某家庭记录了未使用节水龙头 天的日用水量数据(单位: )和使用了节水龙头 天的日用水量数据,得到频数分布表如下:
未使用节水龙头 天的日用水量频数分布表
日用水量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
使用了节水龙头 天的日用水量频数分布表
日用水量 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)在答题卡上作出使用了节水龙头 天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于 的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按 天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
(本小题共12分)
在直角坐标系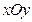 中,动点P到两定点
中,动点P到两定点 ,
,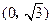 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为 ,过点
,过点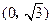 的直线与
的直线与 交于A,B两点.
交于A,B两点.
(1)写出 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在,求出d的最大值、最小值.
(本小题共12分)
甲、乙两个射手进行射击训练,甲击中目标的概率为 ,乙击中目标的概率为
,乙击中目标的概率为 ,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.
,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.
(1)求一个“单位射击组”为“单位进步组”的概率;
(2)记完成三个“单位射击组”后出现“单位进步组”的次数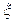 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
(本小题共12分)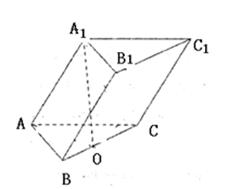
在三棱柱ABC—A1B1C1中,底面是边长为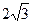 的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
(1)求证:面A1AO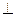 面BCC1B1;
面BCC1B1;
(2)当AA1与底面成45°角时,求二面角A1—AC—B的大小;
(3)若D为侧棱AA1上一点,当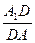 为何值时,BD⊥A1C1.
为何值时,BD⊥A1C1.
(本小题共10分)
已知锐角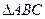 的三内角A、B、C的对边分别是
的三内角A、B、C的对边分别是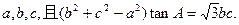
(1)求角A的大小;
(2)求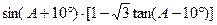 的值.
的值.
设函数

(1)当 时,求函数
时,求函数 在
在 上的最大值;
上的最大值;
(2)记函数 ,若函数
,若函数 有零点,求
有零点,求 的取值范围.
的取值范围.