某工厂的某种产品成箱包装,每箱 件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取 件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为 ,且各件产品是否为不合格品相互独立.
(1)记 件产品中恰有 件不合格品的概率为 ,求 的最大值点 ;
(2)现对一箱产品检验了 件,结果恰有 件不合格品,以(1)中确定的 作为 的值.已知每件产品的检验费用为 元,若有不合格品进入用户手中,则工厂要对每件不合格品支付 元的赔偿费用.
(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为 ,求 ;
(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
(本题满分14分)已知函数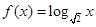 ,且数列
,且数列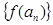 是首项为
是首项为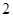 ,公差为2的等差数列.
,公差为2的等差数列.
(1)求证:数列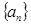 是等比数列;
是等比数列;
(2)设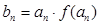 ,求数列
,求数列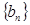 的前
的前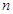 项和
项和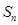 的最小值..
的最小值..
(本题满分14分)如图所示,圆柱的高为2,底面半径为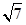 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过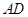 作圆柱的截面交下底面于
作圆柱的截面交下底面于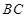 .
.
(1)求证: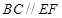 ;
;
(2)若四边形ABCD是正方形,求证 ;
;
(3)在(2)的条件下,求四棱锥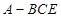 的体积.
的体积.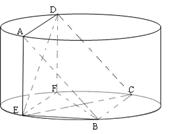
(本题满分12分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
(3)为了研究喜欢打蓝球是否与性别有关,计算出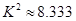 ,你有多大的把握认为是否喜欢打蓝球与性别有关?
,你有多大的把握认为是否喜欢打蓝球与性别有关?
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本题满分12分)已知函数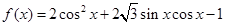 .
.
(1)求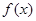 的周期和单调递增区间;
的周期和单调递增区间;
(2)说明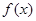 的图象可由
的图象可由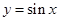 的图象经过怎样变化得到.
的图象经过怎样变化得到.
(本小题满分13分)已知A(0,2,3),B(-2,1,6),C(1,-1,5)
(1)求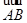 、
、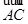 、
、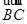 ;
;
(2)求以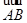 、
、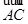 为边的平行四边形的面积;
为边的平行四边形的面积;