如图,四面体 ABCD中, 是正三角形, 是直角三角形, .

(1)证明: ;
(2)过 AC的平面交 BD于点 E,若平面 AEC把四面体 ABCD分成体积相等的两部分,求二面角 的余弦值.
如图,过点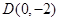 作抛物线
作抛物线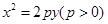 的切线
的切线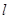 ,切点
,切点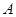 在第二象限.
在第二象限.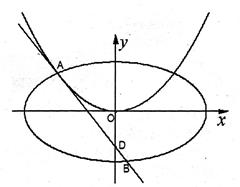
(1)求切点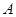 的纵坐标;
的纵坐标;
(2)若离心率为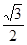 的椭圆
的椭圆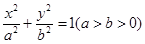 恰好经过切点
恰好经过切点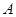 ,设切线
,设切线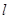 交椭圆的另一点为
交椭圆的另一点为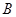 ,记切线
,记切线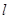 ,
,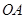 ,
, 的斜率分别为
的斜率分别为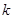 ,
,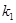 ,
,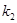 ,若
,若 ,求椭圆方程.
,求椭圆方程.
已知数列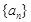 满足:
满足: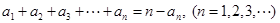 .
.
(1)求证:数列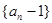 是等比数列;
是等比数列;
(2)令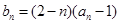 (
(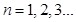 ),如果对任意
),如果对任意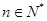 ,都有
,都有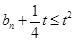 ,求实数
,求实数 的取值范围.
的取值范围.
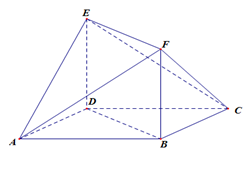
如图,菱形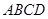 与矩形
与矩形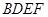 所在平面互相垂直,
所在平面互相垂直,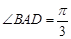 .
.
(1)求证: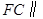 平面
平面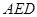 ;
;
(2)若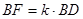 ,当二面角
,当二面角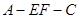 为直二面角时,求
为直二面角时,求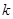 的值;
的值;
(3)在(2)的条件下,求直线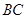 与平面
与平面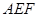 所成的角
所成的角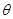 的正弦值.
的正弦值.
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.
(1)从这16人中随机选取3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望,并求出至多有1人是“极幸福”的概率;
的分布列及数学期望,并求出至多有1人是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的数学期望.
的数学期望.
已知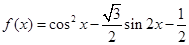 ,
,
(1)写出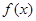 图像的对称中心的坐标和单调递增区间;
图像的对称中心的坐标和单调递增区间;
(2) 三个内角
三个内角 、
、 、
、 所对的边为
所对的边为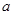 、
、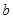 、
、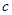 ,若
,若 ,
,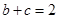 .求
.求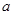 的最小值.
的最小值.