双曲线 ,圆 在第一象限交点为A, ,曲线 。
(1)若 ,求b;
(2)若 , 与x轴交点记为 ,P是曲线 上一点,且在第一象限,并满足 ,求∠ ;
(3)过点 且斜率为 的直线 交曲线 于M、N两点,用b的代数式表示 ,并求出 的取值范围。

设递增等差数列 的前
的前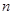 项和为
项和为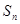 ,已知
,已知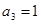 ,
, 是
是 和
和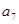 的等比中项.
的等比中项.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前
的前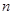 项和
项和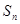 .
.
已知函数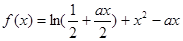
 >0)
>0)
(1)若 的一个极值点,求
的一个极值点,求 的值;
的值;
(2) 上是增函数,求a的取值范围
上是增函数,求a的取值范围
(3)若对任意的 总存在
总存在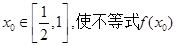 >
>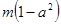 成立,求实数m的取值范围
成立,求实数m的取值范围
定义在区间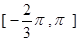 上的函数
上的函数 的图象关于直线
的图象关于直线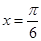 对称,当
对称,当 时函数
时函数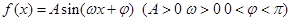 图象如图所示
图象如图所示
(Ⅰ)求函数 在
在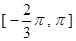 的表达式;
的表达式;
(Ⅱ)求方程 的解;
的解;
(Ⅲ)是否存在常数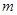 的值,使得
的值,使得 在
在 上恒成立;若存在,求出
上恒成立;若存在,求出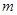 的取值范围;若不存在,请说明理由
的取值范围;若不存在,请说明理由
已知函数f(x)=  是奇函数
是奇函数
(1)求实数m的值
(2)若函数f(x)在区间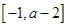 上单调递增,求实数a的取值范围
上单调递增,求实数a的取值范围
已知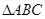 中,
中, ,
,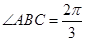 ,设
,设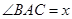 ,并记
,并记
(1)求函数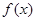 的解析式及其定义域;
的解析式及其定义域;
(2)设函数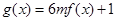 ,若函数
,若函数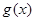 的值域为
的值域为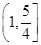 ,试求正实数
,试求正实数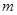 的值
的值